Quickstart

1 Introduction

The bonsaiforest2 package consists of 3 core functions which are typically called in sequence:

run_brms_analysis() - Prepares the model formula and fits the Bayesian model using brms.
summary_subgroup_effects() - Calculates the marginal subgroup treatment effects.
plot() - Creates a forest plot from the summary object.

The package enables the implementation of both global models (Wolbers et al. 2025), that estimate all prognostic and predictive effects in a single unified model using colon notation (e.g., ~ 0 + trt:subgroup), and one-way models (Wang et al. 2024), that estimate treatment slopes varying by subgroup using random effects notation (e.g., ~ (0 + trt || subgroup)).

This vignette demonstrates how to use the package to fit and compare these different modeling formulas. You’ll learn how to:

Fit one-way models (random effects with treatment slopes varying by subgroup)
Fit global models (all subgroup variables in one unified model)
Generate summaries of subgroup treatment effects
Visualize and compare results from different model specifications

This example makes use of Bayesian modeling, which requires the installation of the brms package and a working Stan installation (e.g., via cmdstanr).

2 The Data

We will use a simulated example dataset with a continuous response variable. The relevant outcome is y.

We consider a model where we want to find the treatment effect (trt) on y. The model will adjust for baseline as a prognostic variable (predictor of the outcome) and explore multiple subgroup variables as predictive variables (potential treatment effect modifiers):

X1: Subgroup 1 (categories: A, B, C)
X2: Subgroup 2 (categories: A, B)
X3: Subgroup 3 (categories: A, B, C)
X4: Subgroup 4 (categories: A, B)
X5: Subgroup 5 (categories: A, B)

First, let’s load the libraries and create the data.

# Load the main package
library(bonsaiforest2)
library(brms)

# Create the example data with multiple subgroup variables and treatment effects
set.seed(123)
n <- 500

data <- data.frame(
  id = 1:n,
  trt = rep(0:1, length.out = n),  # Numeric treatment 0/1
  baseline = rnorm(n, mean = 100, sd = 15),
  X1 = factor(sample(c("A", "B", "C"), n, replace = TRUE)),
  X2 = factor(sample(c("A", "B"), n, replace = TRUE)),
  X3 = factor(sample(c("A", "B", "C"), n, replace = TRUE)),
  X4 = factor(sample(c("A", "B"), n, replace = TRUE)),
  X5 = factor(sample(c("A", "B"), n, replace = TRUE))
)

# Generate outcome with baseline effect and heterogeneous treatment effects
data$y <- 50 + 
  0.2 * data$baseline + 
  data$trt * (-5 +                                    # Base treatment effect
    2 * (as.numeric(data$X1 == "A") - 0.33) +        # Heterogeneity by X1
    1.5 * (as.numeric(data$X3 == "B") - 0.33)        # Heterogeneity by X3
  ) + 
  rnorm(n, 0, 10)

print(head(data))
#>   id trt  baseline X1 X2 X3 X4 X5        y
#> 1  1   0  91.59287  A  B  C  B  A 63.61448
#> 2  2   1  96.54734  B  B  C  B  B 70.01582
#> 3  3   0 123.38062  C  A  B  A  B 51.31665
#> 4  4   1 101.05763  B  B  C  A  B 75.00897
#> 5  5   0 101.93932  C  A  C  B  A 54.71636
#> 6  6   1 125.72597  A  B  C  B  B 71.20951

3 One-way Models

This section demonstrates how to fit separate models, each examining one subgroup variable at a time. In one-way models, we specify treatment effects as random slopes using pipe-pipe notation (e.g., ~ (0 + trt || subgroup)), which allows treatment effects to vary by subgroup with automatic hierarchical regularization via random effects.

3.1 One-way Model: X1 Only

# Fit model with only X1 as subgroup variable using one-way approach
# Random effects notation (0 + trt || X1) estimates varying treatment slopes by X1
oneway_X1 <- run_brms_analysis(
  data = data,
  response_type = "continuous",
  response_formula = y ~ trt,
  unshrunk_terms_formula = ~ baseline,
  shrunk_prognostic_formula = NULL,
  shrunk_predictive_formula = ~ (0 + trt || X1),
  intercept_prior = "normal(0, 10)",
  unshrunk_prior = "normal(0, 2.5)",
  shrunk_predictive_prior = set_prior("normal(0, 1)", class = "sd"),
  chains = 2, iter = 2000, warmup = 1000, cores = 2,
  refresh = 0, backend = "cmdstanr"
)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 1 finished in 3.1 seconds.
#> Chain 2 finished in 3.4 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 3.2 seconds.
#> Total execution time: 3.5 seconds.

summary_oneway_X1 <- summary_subgroup_effects(brms_fit = oneway_X1)
print(summary_oneway_X1)
#> $estimates
#> # A tibble: 3 × 4
#>   Subgroup Median CI_Lower CI_Upper
#>   <chr>     <dbl>    <dbl>    <dbl>
#> 1 X1: A     -3.39    -5.31    -1.20
#> 2 X1: B     -3.80    -5.79    -1.72
#> 3 X1: C     -4.91    -7.29    -2.84
#> 
#> $response_type
#> [1] "continuous"
#> 
#> $ci_level
#> [1] 0.95
#> 
#> $trt_var
#> [1] "trt"
#> 
#> attr(,"class")
#> [1] "subgroup_summary"

3.2 One-way Model: X2 Only

oneway_X2 <- run_brms_analysis(
  data = data,
  response_type = "continuous",
  response_formula = y ~ trt,
  unshrunk_terms_formula = ~ baseline,
  shrunk_prognostic_formula = NULL,
  shrunk_predictive_formula = ~ (0 + trt || X2),
  intercept_prior = "normal(0, 10)",
  unshrunk_prior = "normal(0, 2.5)",
  shrunk_predictive_prior = set_prior("normal(0, 1)", class = "sd"),
  chains = 2, iter = 2000, warmup = 1000, cores = 2,
  refresh = 0, backend = "cmdstanr"
)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 2 finished in 3.0 seconds.
#> Chain 1 finished in 3.2 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 3.1 seconds.
#> Total execution time: 3.3 seconds.

summary_oneway_X2 <- summary_subgroup_effects(brms_fit = oneway_X2)

3.3 One-way Model: X3 Only

oneway_X3 <- run_brms_analysis(
  data = data,
  response_type = "continuous",
  response_formula = y ~ trt,
  unshrunk_terms_formula = ~ baseline,
  shrunk_prognostic_formula = NULL,
  shrunk_predictive_formula = ~ (0 + trt || X3),
  intercept_prior = "normal(0, 10)",
  unshrunk_prior = "normal(0, 2.5)",
  shrunk_predictive_prior = set_prior("normal(0, 1)", class = "sd"),
  chains = 2, iter = 2000, warmup = 1000, cores = 2,
  refresh = 0, backend = "cmdstanr"
)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 2 finished in 3.1 seconds.
#> Chain 1 finished in 3.5 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 3.3 seconds.
#> Total execution time: 3.6 seconds.

summary_oneway_X3 <- summary_subgroup_effects(brms_fit = oneway_X3)

3.4 One-way Model: X4 Only

oneway_X4 <- run_brms_analysis(
  data = data,
  response_type = "continuous",
  response_formula = y ~ trt,
  unshrunk_terms_formula = ~ baseline,
  shrunk_prognostic_formula = NULL,
  shrunk_predictive_formula = ~ (0 + trt || X4),
  intercept_prior = "normal(0, 10)",
  unshrunk_prior = "normal(0, 2.5)",
  shrunk_predictive_prior = set_prior("normal(0, 1)", class = "sd"),
  chains = 2, iter = 2000, warmup = 1000, cores = 2,
  refresh = 0, backend = "cmdstanr"
)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 1 finished in 3.3 seconds.
#> Chain 2 finished in 3.6 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 3.5 seconds.
#> Total execution time: 3.7 seconds.

summary_oneway_X4 <- summary_subgroup_effects(brms_fit = oneway_X4)

3.5 One-way Model: X5 Only

oneway_X5 <- run_brms_analysis(
  data = data,
  response_type = "continuous",
  response_formula = y ~ trt,
  unshrunk_terms_formula = ~ baseline,
  shrunk_prognostic_formula = NULL,
  shrunk_predictive_formula = ~ (0 + trt || X5),
  intercept_prior = "normal(0, 10)",
  unshrunk_prior = "normal(0, 2.5)",
  shrunk_predictive_prior = set_prior("normal(0, 1)", class = "sd"),
  chains = 2, iter = 2000, warmup = 1000, cores = 2,
  refresh = 0, backend = "cmdstanr"
)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 2 finished in 3.5 seconds.
#> Chain 1 finished in 3.8 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 3.7 seconds.
#> Total execution time: 3.8 seconds.

summary_oneway_X5 <- summary_subgroup_effects(brms_fit = oneway_X5)

3.6 One-way Models: Visualizing All Models

You can combine and visualize results from multiple models using combine_summaries():

# Combine all one-way models
combined_oneway <- combine_summaries(list(
  "X1" = summary_oneway_X1,
  "X2" = summary_oneway_X2,
  "X3" = summary_oneway_X3,
  "X4" = summary_oneway_X4,
  "X5" = summary_oneway_X5
))

plot(combined_oneway, title = "One-way Models: All Subgroup Variables")
#> Preparing data for plotting...
#> Generating plot...
#> Done.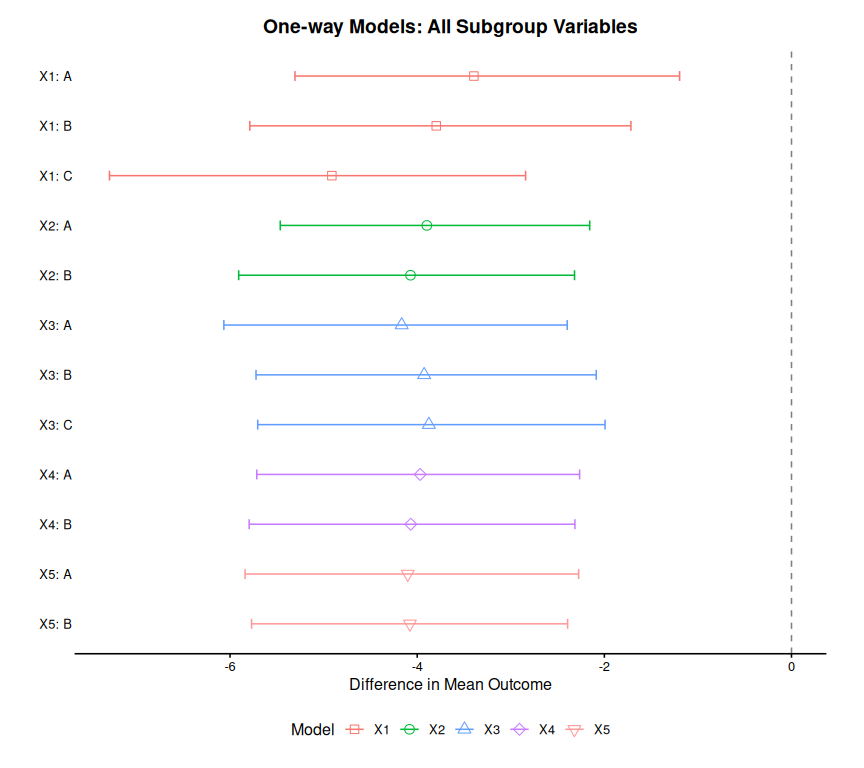

4 Global Model

This section demonstrates how to fit a single model that includes all subgroup variables simultaneously using the global approach. All treatment-by-subgroup interactions are estimated in one unified model with colon notation (e.g., ~ 0 + trt:subgroup) and strong regularization (Horseshoe prior) applied to the interaction terms.

4.1 Global Model: All Subgroups

# Fit a single unified model with ALL subgroup variables simultaneously using global approach
# - Unshrunk terms: baseline with reference coding
# - Shrunk prognostic effects: subgroup main effects with strong regularization using one-hot encoding
# - Shrunk predictive effects: treatment interactions with strong regularization using one-hot encoding
global_shrinkage_model <- run_brms_analysis(
  data = data,
  response_type = "continuous",
  response_formula = y ~ trt,
  unshrunk_terms_formula = ~ baseline,
  shrunk_prognostic_formula = ~ 0 + X1 + X2 + X3 + X4 + X5,
  shrunk_predictive_formula = ~ 0 + trt:X1 + trt:X2 + trt:X3 + trt:X4 + trt:X5,
  intercept_prior = "normal(0, 10)",
  unshrunk_prior = "normal(0, 2.5)",
  shrunk_prognostic_prior = "horseshoe(scale_global = 1)",
  shrunk_predictive_prior = "horseshoe(scale_global = 0.5)",
  chains = 2, iter = 2000, warmup = 1000, cores = 2,
  refresh = 0, backend = "cmdstanr"
)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 2 finished in 8.6 seconds.
#> Chain 1 finished in 8.9 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 8.7 seconds.
#> Total execution time: 9.0 seconds.

4.2 Global Model: Summary of Subgroup Effects

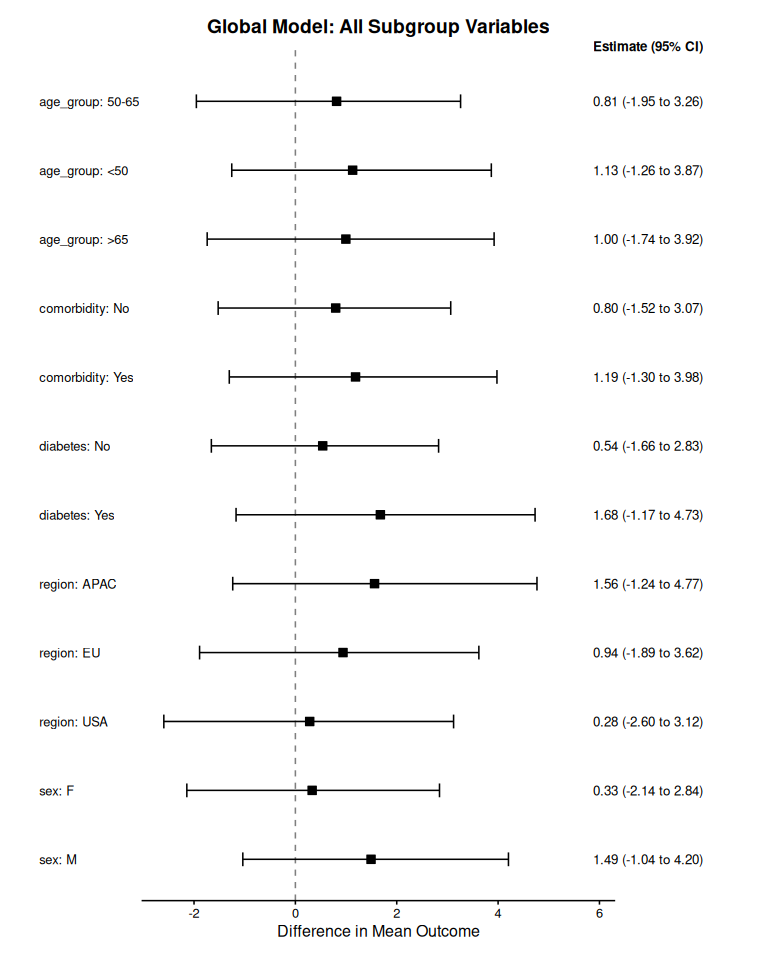
Use summary_subgroup_effects() to generate marginal treatment effects for each subgroup. The function automatically extracts all treatment interactions from the fitted model:

global_summary <- summary_subgroup_effects(brms_fit = global_shrinkage_model)
#> --- Calculating specific subgroup effects... ---
#> Step 1: Identifying subgroups and creating counterfactuals...
#> ...detected subgroup variable(s): X1, X2, X3, X4, X5
#> Step 2: Generating posterior predictions...
#> Step 3: Calculating marginal effects...
#> Done.

# Print the summary of subgroup-specific treatment effects
print(global_summary)
#> $estimates
#> # A tibble: 12 × 4
#>    Subgroup Median CI_Lower CI_Upper
#>    <chr>     <dbl>    <dbl>    <dbl>
#>  1 X1: A     -3.66    -5.75    -1.47
#>  2 X1: B     -3.84    -5.86    -1.77
#>  3 X1: C     -4.96    -7.50    -2.90
#>  4 X2: A     -4.21    -6.22    -2.32
#>  5 X2: B     -4.09    -6.12    -2.20
#>  6 X3: A     -4.71    -7.22    -2.52
#>  7 X3: B     -3.91    -6.01    -1.67
#>  8 X3: C     -3.92    -5.94    -1.83
#>  9 X4: A     -4.19    -6.09    -2.31
#> 10 X4: B     -4.10    -6.16    -2.26
#> 11 X5: A     -4.18    -6.20    -2.35
#> 12 X5: B     -4.14    -6.04    -2.26
#> 
#> $response_type
#> [1] "continuous"
#> 
#> $ci_level
#> [1] 0.95
#> 
#> $trt_var
#> [1] "trt"
#> 
#> attr(,"class")
#> [1] "subgroup_summary"

4.3 Global Model: Visualization

Use the plot() function to create a forest plot from the summary object:

plot(global_summary, title = "Global Model: All Subgroup Variables")
#> Preparing data for plotting...
#> Generating plot...
#> Done.

5 Comparing Multiple Models in One Plot

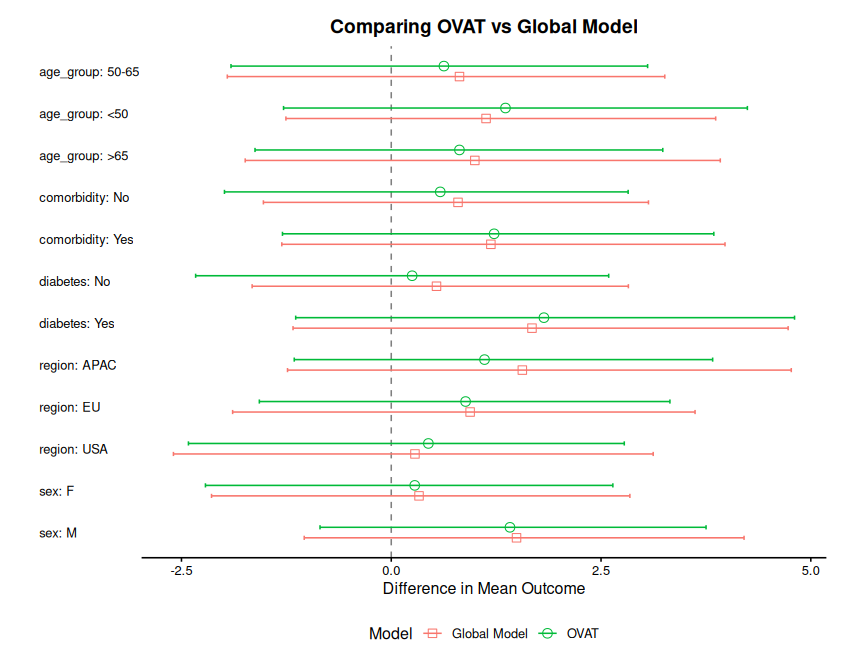
The plot() function supports comparing multiple models side-by-side. Pass a named list of subgroup_summary objects to create a comparative forest plot.

5.1 Example: Comparing One-way vs Global Models

# Combine summaries for comparison
combined <- combine_summaries(list(
  "One-way" = combined_oneway,
  "Global" = global_summary
))

# Plot the comparison
plot(combined, title = "Comparing One-way vs Global Models")
#> Preparing data for plotting...
#> Generating plot...
#> Done.

Wang, Yun, Wenda Tu, William Koh, James Travis, Robert Abugov, Kiya Hamilton, Mengjie Zheng, Roberto Crackel, Pablo Bonangelino, and Mark Rothmann. 2024. “Bayesian hierarchical models for subgroup analysis.” Pharmaceutical Statistics 23: 1065–83.

Wolbers, Marcel, Mar Vázquez Rabuñal, Ke Li, Kaspar Rufibach, and Daniel Sabanés Bové. 2025. “Using shrinkage methods to estimate treatment effects in overlapping subgroups in randomized clinical trials with a time-to-event endpoint.” Statistical Methods in Medical Research, 1–12.

Miriam Pedrera Gomez, Isaac Gravestock, and Marcel Wolbers