Calculate dose estimates for a fitted dose-response model (via fitMod, bFitMod) or maFitMod) or a Mods object

The TD (target dose) is defined as the dose that achieves a target effect of Delta over placebo (if there are multiple such doses, the smallest is chosen):

$$TD_\Delta = \min \{x|f(x) > f(0)+\Delta\}$$

If a decreasing trend is beneficial the definition of the TD is

$$TD_\Delta = \min \{x|f(x) < f(0)-\Delta\}$$

When \(\Delta\) is the clinical relevance threshold, then the TD is similar to the usual definition of the minimum effective dose (MED).

The ED (effective dose) is defined as the dose that achieves a certain percentage p of the full effect size (within the observed dose-range!) over placebo (if there are multiple such doses, the smallest is chosen). $$ED_p=\min\{x|f(x) > f(0) + p(f(dmax)-f(0))$$

Note that this definition of the EDp is different from traditional definition based on the Emax model, where the EDp is defined relative to the asymptotic maximum effect (rather than the maximum effect in the observed dose-range).

ED or TD calculation for bootstrap model averaging (maFit) objects is based on first calculating the pointwise median dose-response curve estimate. Then calculating the dose estimate based on this curve.

Usage

TD(
  object,
  Delta,
  TDtype = c("continuous", "discrete"),
  direction = c("increasing", "decreasing"),
  doses = NULL
)

ED(
  object,
  p,
  EDtype = c("continuous", "discrete"),
  direction = c("increasing", "decreasing"),
  doses = NULL
)

Arguments

object

An object of class c(Mods, fullMod), DRMod, bFitMod or maFit

Delta, p

Delta: The target effect size use for the target dose (TD) (Delta should be > 0).

p: The percentage of the dose to use for the effective dose.

TDtype, EDtype

character that determines, whether the dose should be treated as a continuous variable when calculating the TD/ED or whether the TD/ED should be calculated based on a grid of doses specified in doses

direction

Direction to be used in defining the TD. This depends on whether an increasing or decreasing of the response variable is beneficial. In case of ED calculation only needed for maFit objects.

doses

Dose levels to be used if TDtype or EDtype are equal to "discrete". Needs to include placebo, and may not exceed the dose range of the model(s) provided in object.

Value

Returns the dose estimate

See also

Mods, drmodels, fitMod, bFitMod

Author

Bjoern Bornkamp

Examples

## example for creating a "full-model" candidate set placebo response
## and maxEff already fixed in Mods call
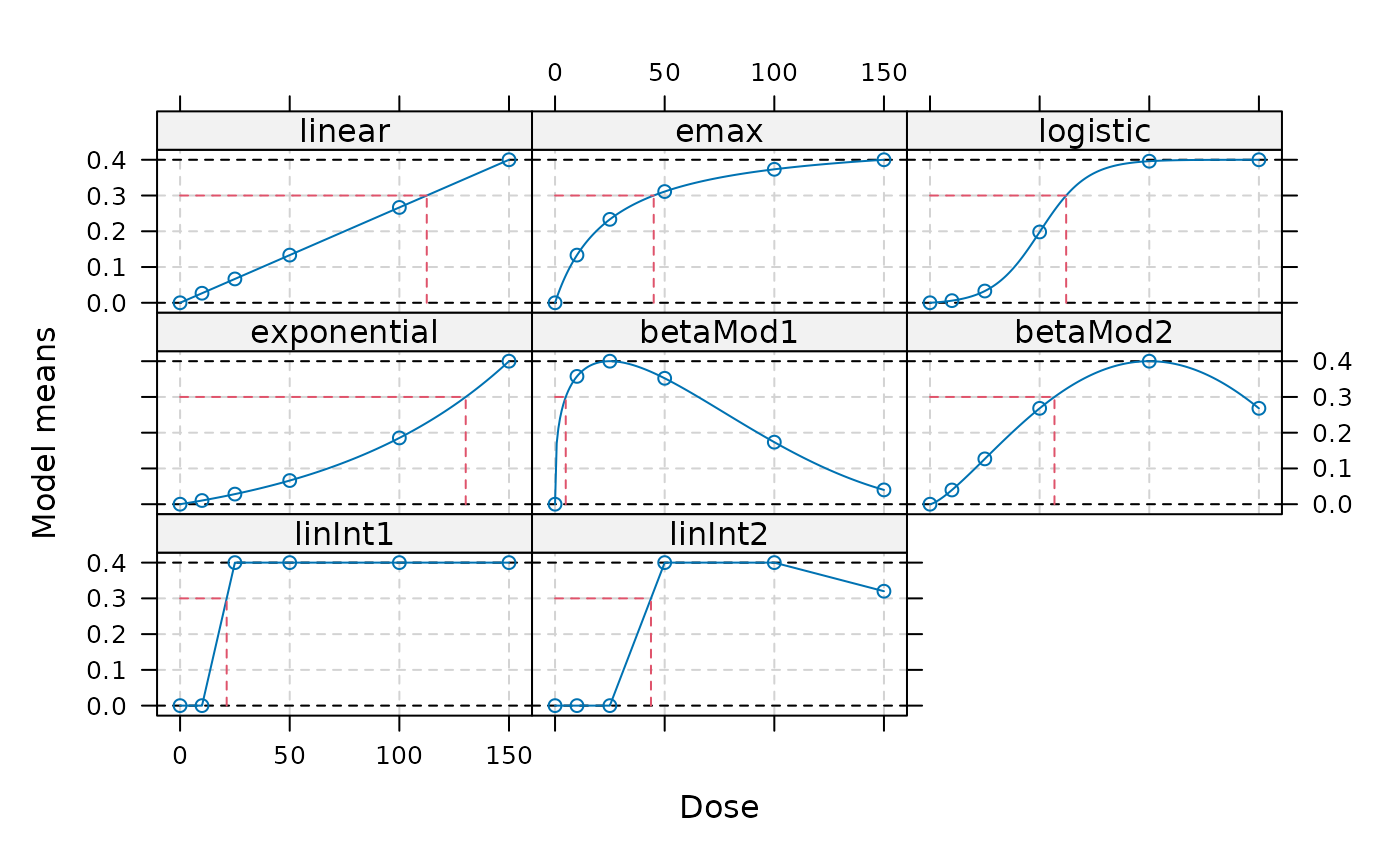
doses <- c(0, 10, 25, 50, 100, 150)
fmodels <- Mods(linear = NULL, emax = 25,
                logistic = c(50, 10.88111), exponential = 85,
                betaMod = rbind(c(0.33, 2.31), c(1.39, 1.39)),
                linInt = rbind(c(0, 1, 1, 1, 1),
                               c(0, 0, 1, 1, 0.8)),
                doses=doses, placEff = 0, maxEff = 0.4,
                addArgs=list(scal=200))
## calculate doses giving an improvement of 0.3 over placebo
TD(fmodels, Delta=0.3)
#>      linear        emax    logistic exponential    betaMod1    betaMod2 
#>  112.500000   45.000000   62.095220  130.265330    4.880978   56.762044 
#>     linInt1     linInt2 
#>   21.250000   43.750000 
## discrete version
TD(fmodels, Delta=0.3, TDtype = "discrete", doses=doses)
#>      linear        emax    logistic exponential    betaMod1    betaMod2 
#>         150          50         100         150          10         100 
#>     linInt1     linInt2 
#>          25          50 
## doses giving 50% of the maximum effect
ED(fmodels, p=0.5)
#>      linear        emax    logistic exponential    betaMod1    betaMod2 
#>   75.000000   18.750000   50.215409  104.517639    1.255838   37.337384 
#>     linInt1     linInt2 
#>   17.500000   37.500000 
ED(fmodels, p=0.5, EDtype = "discrete", doses=doses)
#>      linear        emax    logistic exponential    betaMod1    betaMod2 
#>         100          25         100         150          10          50 
#>     linInt1     linInt2 
#>          25          50 
plot(fmodels, plotTD = TRUE, Delta = 0.3)