Construct a Minimally Informative Prior

This function constructs a minimally informative prior, which is captured in a LogisticNormal (or LogisticLogNormal) object.

Based on the proposal by Neuenschwander et al (2008, Statistics in Medicine), a minimally informative prior distribution is constructed. The required key input is the minimum (\(d_{1}\) in the notation of the Appendix A.1 of that paper) and the maximum value (\(d_{J}\)) of the dose grid supplied to this function. Then threshmin is the probability threshold \(q_{1}\), such that any probability of DLT larger than \(q_{1}\) has only 5% probability. Therefore \(q_{1}\) is the 95% quantile of the beta distribution and hence \(p_{1} = 0.95\). Likewise, threshmax is the probability threshold \(q_{J}\), such that any probability of DLT smaller than \(q_{J}\) has only 5% probability (\(p_{J} = 0.05\)). The probabilities \(1 - p_{1}\) and \(p_{J}\) can be controlled with the arguments probmin and probmax, respectively. Subsequently, for all doses supplied in the dosegrid argument, beta distributions are set up from the assumption that the prior medians are linear in log-dose on the logit scale, and Quantiles2LogisticNormal() is used to transform the resulting quantiles into an approximating LogisticNormal (or LogisticLogNormal) model. Note that the reference dose is not required for these computations.

Usage

MinimalInformative(
  dosegrid,
  refDose,
  threshmin = 0.2,
  threshmax = 0.3,
  probmin = 0.05,
  probmax = 0.05,
  ...
)

Arguments

dosegrid

(numeric)
the dose grid.

refDose

(number)
the reference dose.

threshmin

(number)
any toxicity probability above this threshold would be very unlikely (see probmin) at the minimum dose.

threshmax

(number)
any toxicity probability below this threshold would be very unlikely (see probmax) at the maximum dose.

probmin

(number)
the prior probability of exceeding threshmin at the minimum dose.

probmax

(number)
the prior probability of being below threshmax at the maximum dose.

...

additional arguments for computations, see Quantiles2LogisticNormal(), e.g. refDose and logNormal=TRUE to obtain a minimal informative log normal prior.

Value

See Quantiles2LogisticNormal().

Examples

# \donttest{
# Setting up a minimal informative prior 
# max.time is quite small only for the purpose of showing the example. They 
# should be increased for a real case.
set.seed(132)
coarseGrid <- c(0.1, 10, 30, 60, 100)
minInfModel <- MinimalInformative(dosegrid = coarseGrid,
                                  refDose=50,
                                  threshmin=0.2,
                                  threshmax=0.3,
                                  control=## for real case: leave out control 
                                    list(max.time=0.1)) 
#> It: 1, obj value (lsEnd): 0.6732911061 indTrace: 1
#> timeSpan = 4.547537 maxTime = 0.1
#> Emini is: 0.6732911061
#> xmini are:
#> 3.436837973 9.074768474 4.306636605 0.7253533934 -0.7572128108 
#> Totally it used 4.547566 secs
#> No. of function call is: 991

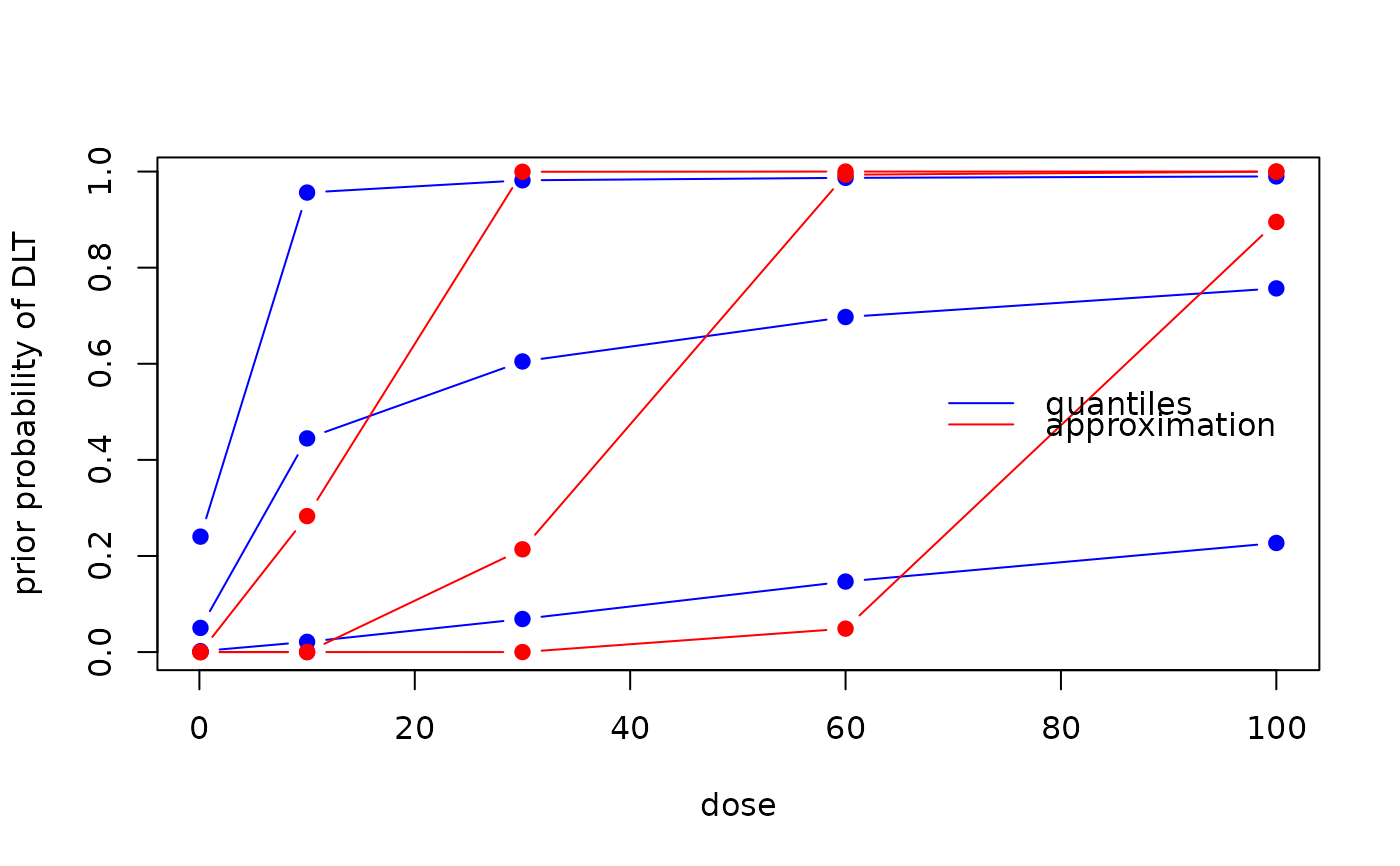
# Plotting the result
matplot(x=coarseGrid,
        y=minInfModel$required,
        type="b", pch=19, col="blue", lty=1,
        xlab="dose",
        ylab="prior probability of DLT")
matlines(x=coarseGrid,
         y=minInfModel$quantiles,
         type="b", pch=19, col="red", lty=1)
legend("right",
       legend=c("quantiles", "approximation"),
       col=c("blue", "red"),
       lty=1,
       bty="n")

# }