Ordinal CRM

library(crmPack)
#> Loading required package: ggplot2
#> Registered S3 method overwritten by 'crmPack':
#>   method       from  
#>   print.gtable gtable
#> Type crmPackHelp() to open help browser
#> Type crmPackExample() to open example

Introduction

The original CRM model introduced by (O’Quigley, Pepe, and Fisher 1990) dichotomises toxicity events as either “Not toxic” or “DLT”. The ordinal CRM generalises this model by classifying toxicities on an ordinal scale with an arbitrary number of categories (though use of more than three or four would be unusual).

This approach is particularly useful in non-oncology settings, where there is a greater interest in adverse events that are not dose limiting but are nonetheless undesirable.

Implementation

Ordinal data

crmPack uses the DataOrdinal class to record data observed during an ordinal CRM trial. The OrdinalData class differs from the Data class only in that it contains an extra slot, yCategories, that defines both the number of toxicity grades and their labels.For example:

empty_ordinal_data <- DataOrdinal(
  doseGrid = c(seq(from = 10, to = 100, by = 10)),
  yCategories = c("No tox" = 0L, "Sub-tox AE" = 1L, "DLT" = 2L),
  placebo = FALSE
)

defines a DataOrdinal object with three toxicity grades, labelled “No tox`”, “Sub-tox AE” and “DLT”.

Note that the yCategories slot must be an integer vector with values ordered from 0 to length(yCategories) - 1. Its labels must be unique. The first entry, which must have value 0, is always regarded as the “no event” category. See [The LogisticLogNormalOrdinal class] below.

The update, plot and dose_grid_range methods work exactly as they do for Data objects:

dose_grid_range(empty_ordinal_data)
#> [1]  10 100

ordinal_data <- update(empty_ordinal_data, x = 10, y = 0)
ordinal_data <- update(ordinal_data, x = 20, y = 0)
ordinal_data <- update(ordinal_data, x = 30, y = 0)
ordinal_data <- update(ordinal_data, x = 40, y = 0)
ordinal_data <- update(ordinal_data, x = 50, y = c(0, 1, 0))
ordinal_data <- update(ordinal_data, x = 60, y = c(0, 1, 2))

plot(ordinal_data)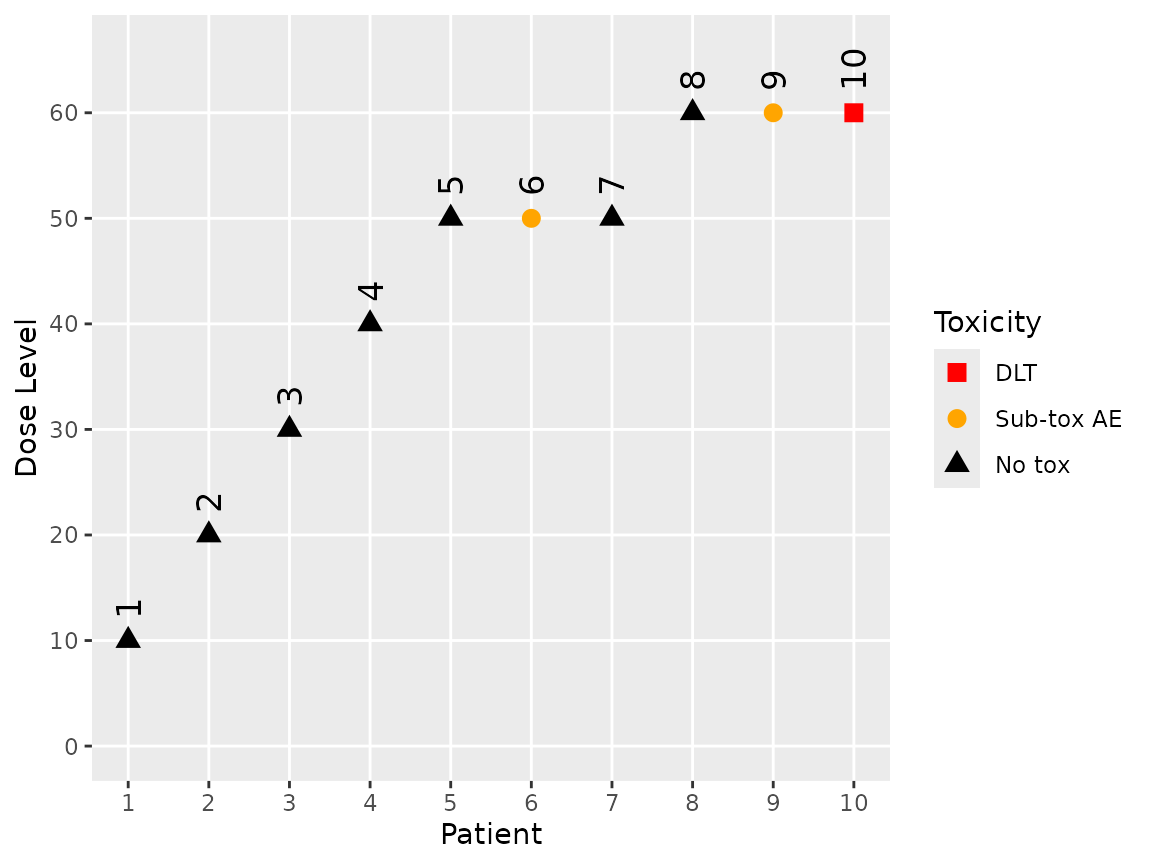

The LogisticLogNormalOrdinal class

crmPack fits a constrained logistic log normal model to ordinal data. The logit of the probability of toxicity at each grade for a given dose is modelled in the log odds space as a linear regression with common slope and a different intercept for each toxicity grade.

Note, unlike other model classes, LogisticLogNormalOrdinal requires a diagonal covariance matrix. This is because the constraints on the $alpha;s - the intercept parameters - imposes a correlation on the model’s parameters. Thus, any covariance structure requested by the end user could not be honoured by the model.

Let p_k(d) be the probability that the response of a patient treated at dose d is in category k or higher, k=0, …, K; d=1, …, D.

Then

$$\log \left( \frac{p}{1-p}\right) = \alpha_k + \beta \cdot \log \left( \frac{d}{d_{ref}} \right)$$ for k=1, …, K [p₀(d) = 1 by definition] where d_ref is a reference dose.

The αs are constrained such that α₁ > α₂ > … > α_K.

The priors for the model’s parameters are:

$$\alpha_k \sim N(\mu_{\alpha_k}, \sigma_{\alpha_k}^2)$$

and

$$\log(\beta) \sim N(\mu_\beta, \sigma_\beta^2)$$

A LogisticLogOrdinal is initialised in exactly the same way as a LogisticLogNormal object:

ordinal_model <- LogisticLogNormalOrdinal(
  mean = c(3, 4, 0),
  cov = diag(c(4, 3, 1)),
  ref_dose = 55
)

The entries in the mean and cov parameters define the hyper priors for α₁ to α_K-1 and β in that order.

Model fitting

mcmc works as expected with ordinal models:

opts <- .DefaultMcmcOptions()

samples <- mcmc(ordinal_data, ordinal_model, opts)
#> Warning in rjags::jags.model(file = model_file, data = model_data, inits =
#> c(model_inits, : Unused variable "y" in data

The warning message is expected and can be ignored. It will be suppressed in a future version of crmPack. See issue 748.

The Samples object returned by mcmc is a standard Samples object. The names of the entries in its data slot are

names(samples@data)
#> [1] "alpha1" "alpha2" "beta"

It can be passed to the fit method, using the grade parameter to specify the toxicity grade for which cumulative probabilities of toxicity are required:

fit(samples, ordinal_model, ordinal_data, grade = 1L)
#>    dose     middle        lower     upper
#> 1    10 0.04080023 8.293901e-10 0.2684245
#> 2    20 0.08050572 3.052626e-06 0.3546002
#> 3    30 0.13711968 4.311721e-04 0.4190757
#> 4    40 0.22186288 1.286292e-02 0.5065647
#> 5    50 0.34792495 1.035482e-01 0.6561853
#> 6    60 0.49381176 1.749951e-01 0.8381525
#> 7    70 0.60216536 1.989343e-01 0.9621558
#> 8    80 0.67159104 2.257074e-01 0.9893601
#> 9    90 0.71802011 2.371611e-01 0.9972199
#> 10  100 0.75104386 2.537747e-01 0.9991609
fit(samples, ordinal_model, ordinal_data, grade = 2L)
#>    dose     middle        lower     upper
#> 1    10 0.02094626 3.838722e-10 0.1448244
#> 2    20 0.04149639 1.891209e-06 0.1979087
#> 3    30 0.07141167 2.182169e-04 0.2566465
#> 4    40 0.11844216 6.370169e-03 0.3228513
#> 5    50 0.19772893 4.878250e-02 0.4343838
#> 6    60 0.31796710 8.587041e-02 0.6623486
#> 7    70 0.43526243 1.085890e-01 0.9003720
#> 8    80 0.52128781 1.195123e-01 0.9756381
#> 9    90 0.58259654 1.306373e-01 0.9933807
#> 10  100 0.62794569 1.458878e-01 0.9980132

The cumulative flag can be used to request grade-specific probabilities.

fit(samples, ordinal_model, ordinal_data, grade = 1L, cumulative = FALSE)
#>    dose     middle        lower     upper
#> 1    10 0.01985397 2.407939e-10 0.1637915
#> 2    20 0.03900933 7.096674e-07 0.2143564
#> 3    30 0.06570802 1.226464e-04 0.2854251
#> 4    40 0.10342072 1.889947e-03 0.3515263
#> 5    50 0.15019601 5.031285e-03 0.4649518
#> 6    60 0.17584465 6.021647e-03 0.5178695
#> 7    70 0.16690293 5.355370e-03 0.4896783
#> 8    80 0.15030323 2.767006e-03 0.4694554
#> 9    90 0.13542357 9.234034e-04 0.4443503
#> 10  100 0.12309817 3.068985e-04 0.4342210
fit(samples, ordinal_model, ordinal_data, grade = 2L, cumulative = FALSE)
#>    dose     middle        lower     upper
#> 1    10 0.02094626 3.838722e-10 0.1448244
#> 2    20 0.04149639 1.891209e-06 0.1979087
#> 3    30 0.07141167 2.182169e-04 0.2566465
#> 4    40 0.11844216 6.370169e-03 0.3228513
#> 5    50 0.19772893 4.878250e-02 0.4343838
#> 6    60 0.31796710 8.587041e-02 0.6623486
#> 7    70 0.43526243 1.085890e-01 0.9003720
#> 8    80 0.52128781 1.195123e-01 0.9756381
#> 9    90 0.58259654 1.306373e-01 0.9933807
#> 10  100 0.62794569 1.458878e-01 0.9980132

Note that, for grade == K - 1, the cumulative and grade-specific probabilities of toxicities are identical.

The plot method also takes grade and cumulative parameters.

plot(samples, ordinal_model, ordinal_data, grade = 2L)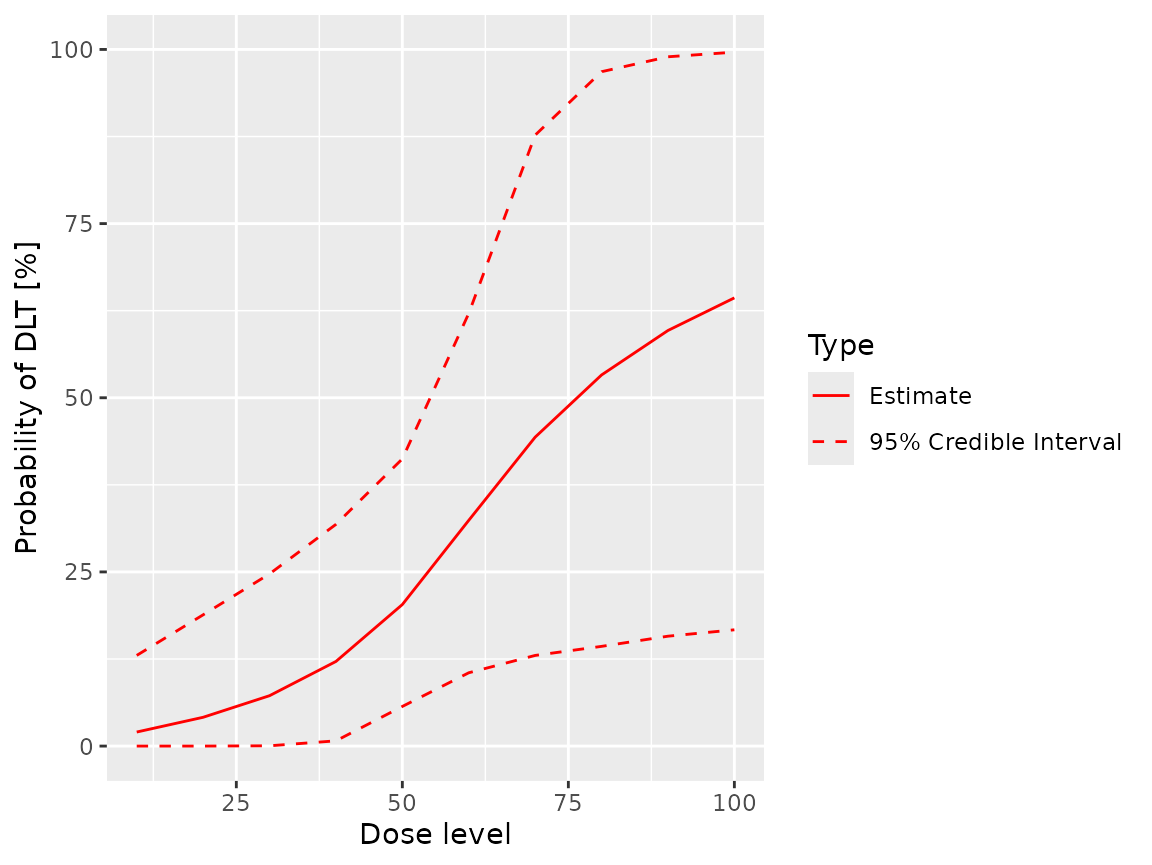

plot(samples, ordinal_model, ordinal_data, grade = 1L)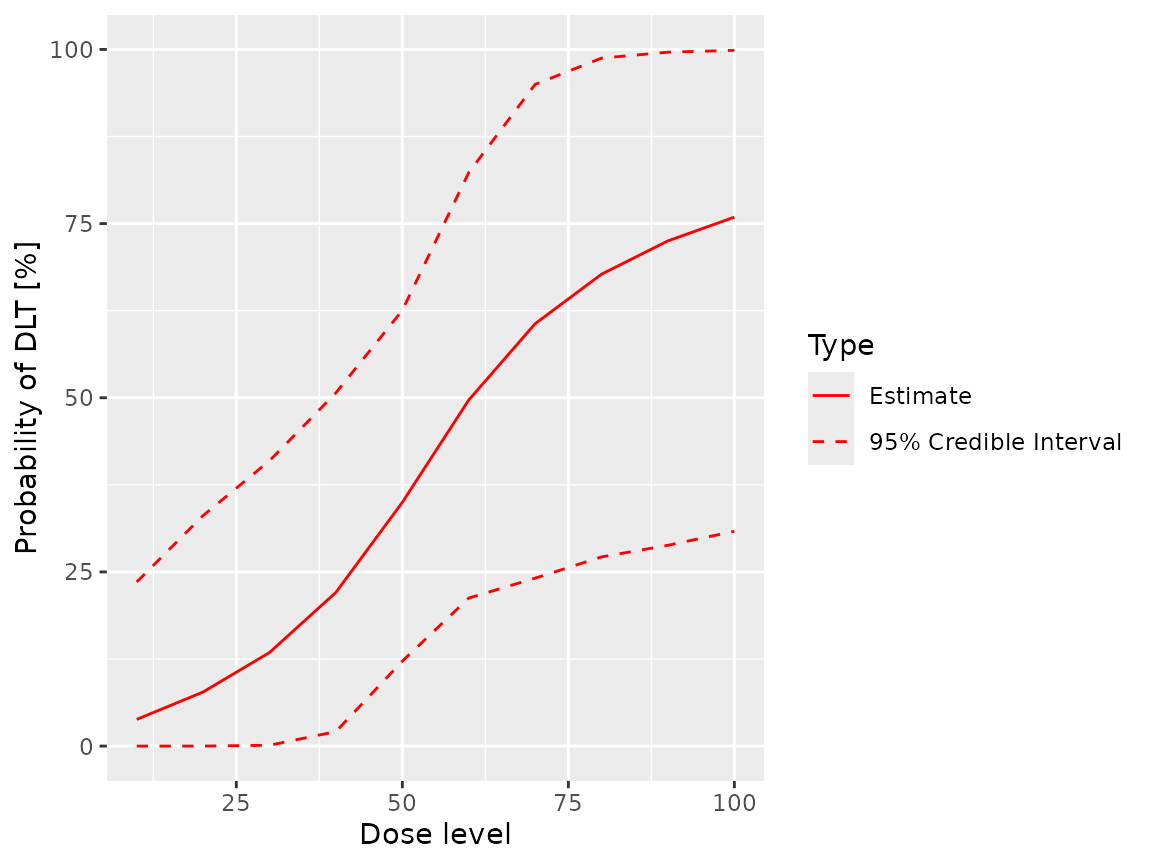

plot(samples, ordinal_model, ordinal_data, grade = 1L, cumulative = FALSE)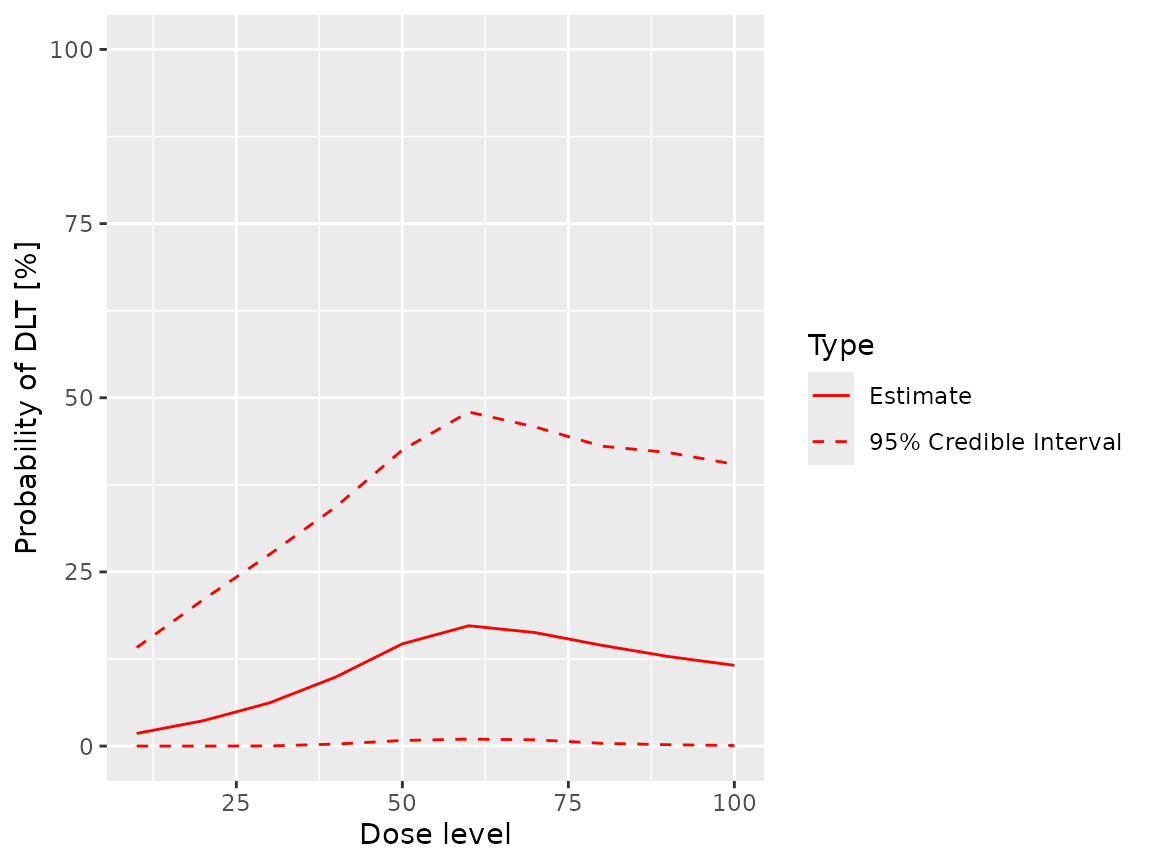

Rules classes for ordinal models

For each class of Rule (that is, CohortSize, Increments, NextBest and Stopping), crmPack provides a single wrapper class that allows the Rule to be applied in trials using ordinal CRM models. The wrapper class has the name <Rule>Ordinal and takes two parameters, rule and grade. rule defines the standard crmPck Rule and grade the toxicity grade at which the rule should be applied.

For example

dlt_rule <- CohortSizeDLT(intervals = 0:2, cohort_size = c(1, 3, 5))
ordinal_rule_1 <- CohortSizeOrdinal(grade = 1L, rule = dlt_rule)
ordinal_rule_2 <- CohortSizeOrdinal(grade = 2L, rule = dlt_rule)

size(ordinal_rule_1, 50, empty_ordinal_data)
#> [1] 1
size(ordinal_rule_2, 50, empty_ordinal_data)
#> [1] 1
size(ordinal_rule_1, 50, ordinal_data)
#> [1] 5
size(ordinal_rule_2, 50, ordinal_data)
#> [1] 3

Rules based on different toxicity grades can be combined to produce complex rules. Here we define two Increments rules, one based on toxicity grade 1, the other on toxicity grade 2. Recall two sub toxic AEs and one DLT have been reported in the example data set.

Thus, the rule based on sub-toxic AEs allows a maximum increment of 0.67 because three events have been reported, giving a maximum permitted dose of 100.2. As only one DLT has been reported, the second rule allows an increment of 0.5, giving a maximum permitted dose of 90.

ordinal_rule_1 <- IncrementsOrdinal(
  grade = 1L,
  rule = IncrementsRelativeDLT(intervals = 0:2, increments = c(3, 1.5, 0.67))
)
maxDose(ordinal_rule_1, ordinal_data)
#> [1] 100.2
ordinal_rule_2 <- IncrementsOrdinal(
  grade = 2L,
  rule = IncrementsRelativeDLT(intervals = 0:1, increments = c(3, 0.5))
)
maxDose(ordinal_rule_2, ordinal_data)
#> [1] 90

The two grade-specific rules can be combined into a single rule using IncrementsMin:

trial_rule <- IncrementsMin(list(ordinal_rule_1, ordinal_rule_2))
maxDose(trial_rule, ordinal_data)
#> [1] 90

On the need for a diagonal covariance matrix

Consider a standard logistic log Normal CRM model:

model <- LogisticLogNormal(
  mean = c(-3, 1),
  cov = matrix(c(4, -0.5, -0.5, 3), ncol = 2),
  ref_dose = 45
)

model@params@cov
#>      [,1] [,2]
#> [1,]  4.0 -0.5
#> [2,] -0.5  3.0

We can estimate the prior using an empty Data object…

data <- Data(doseGrid = seq(10, 100, 10))
options <- McmcOptions(
  samples = 30000,
  rng_kind = "Mersenne-Twister",
  rng_seed = 8191316
)
samples <- mcmc(data, model, options)

and then obtain the correlation between the model’s parameters [recalling that the prior is defined in terms of log(alpha1)]…

d <- as.matrix(cbind(samples@data$alpha0, log(samples@data$alpha1)))
sigmaHat <- cov(d)
sigmaHat
#>            [,1]       [,2]
#> [1,]  4.0094331 -0.5416752
#> [2,] -0.5416752  3.0363958

So we requested a covariance of -0.5 and got -0.5416755.2. Pretty good!

Now look an ordinal CRM model with non-zero correlation between its parameters.

To begin, take a copy of the current LogisticLogNormalOrdinal model and give it a non-diagonal covariance matrix by accessing its params@cov slot directly, deliberately avoiding object validation.

NB This is poor practice and not recommended. It is done here purely for illustration.

ordinal_model_temp <- ordinal_model
ordinal_model_temp@params@cov <- matrix(c(4, -0.5, -0.5, -0.5, 3, -0.5, -0.5, -0.5, 1), ncol = 3)

ordinal_model_temp@params@cov
#>      [,1] [,2] [,3]
#> [1,]  4.0 -0.5 -0.5
#> [2,] -0.5  3.0 -0.5
#> [3,] -0.5 -0.5  1.0

Fit the revised model to obtain the prior.

ordinal_data <- DataOrdinal(doseGrid = seq(10, 100, 10))
ordinal_samples <- mcmc(ordinal_data, ordinal_model_temp, options)
#> Warning in rjags::jags.model(file = model_file, data = model_data, inits =
#> c(model_inits, : Unused variable "tox" in data

Finally, look at the covariance matrix, remembering to use log(beta) rather than beta…

ordinalD <- as.matrix(
  cbind(
    ordinal_samples@data$alpha1,
    ordinal_samples@data$alpha2,
    log(ordinal_samples@data$beta)
  )
)
sigmaHat <- cov(ordinalD)
sigmaHat
#>             [,1]        [,2]         [,3]
#> [1,]  4.00158899 2.768345336 -0.001112980
#> [2,]  2.76834534 2.924696828  0.008697924
#> [3,] -0.00111298 0.008697924  1.012033823

The correlations are nothing like what we requested. This is due to the constraints imposed on the intercepts by the model. The situation will most likely worsen as the number of toxicity categories increases.

We have an open issue - #755 -to examine options for allowing end users to specify correlation structures for ordinal CRM models. If you would like to contribute, please do so.

Some observations

• We are currently considering the need for making grade-specific functionality available across more crmPack methods. If you have a specific use case that is not currently supported, please contact us.
• If you have a need for ordinal CRM in dual endpoint models, please let us know.
• Had crmPack supported ordinal CRM from the outset, the classes that support standard, binary, CRM models would have been sub-classes of the more general ordinal implementations. We did consider taking this approach when adding support for ordinal CRM models to the existing code. We decided against doing so for purely defensive and conservative reasons. Had we introduced the ordinal classes as parents of the existing classes, changes to the code base would have been much more substantial and we were concerned that we might miss some implicit assumptions about the dimensionality of the existing models. We therefore chose to implement ordinal classes as siblings, rather than parents, of the existing classes. This approach minimises the risk of breaking existing end-user code at the risk of slightly greater complexity in using the new classes.

Environment

#> R version 4.5.0 (2025-04-11)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 24.04.2 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0
#> 
#> locale:
#>  [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
#>  [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
#>  [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
#>  [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
#>  [9] LC_ADDRESS=C               LC_TELEPHONE=C            
#> [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       
#> 
#> time zone: Etc/UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] crmPack_2.0.0.9002 ggplot2_4.0.0     
#> 
#> loaded via a namespace (and not attached):
#>  [1] sass_0.4.10          generics_0.1.4       futile.options_1.0.1
#>  [4] xml2_1.4.0           lattice_0.22-7       stringi_1.8.7       
#>  [7] digest_0.6.37        magrittr_2.0.4       evaluate_1.0.5      
#> [10] grid_4.5.0           RColorBrewer_1.1-3   mvtnorm_1.3-3       
#> [13] fastmap_1.2.0        jsonlite_2.0.0       backports_1.5.0     
#> [16] formatR_1.14         gridExtra_2.3        viridisLite_0.4.2   
#> [19] scales_1.4.0         textshaping_1.0.4    jquerylib_0.1.4     
#> [22] cli_3.6.5            rlang_1.1.6          futile.logger_1.4.3 
#> [25] parallelly_1.45.1    withr_3.0.2          cachem_1.1.0        
#> [28] yaml_2.3.10          parallel_4.5.0       tools_4.5.0         
#> [31] coda_0.19-4.1        checkmate_2.3.3      dplyr_1.1.4         
#> [34] lambda.r_1.2.4       kableExtra_1.4.0     vctrs_0.6.5         
#> [37] R6_2.6.1             lifecycle_1.0.4      stringr_1.5.2       
#> [40] GenSA_1.1.14.1       fs_1.6.6             htmlwidgets_1.6.4   
#> [43] ragg_1.5.0           rjags_4-17           pkgconfig_2.0.3     
#> [46] desc_1.4.3           pkgdown_2.1.3        pillar_1.11.1       
#> [49] bslib_0.9.0          gtable_0.3.6         glue_1.8.0          
#> [52] systemfonts_1.3.1    xfun_0.53            tibble_3.3.0        
#> [55] tidyselect_1.2.1     rstudioapi_0.17.1    knitr_1.50          
#> [58] dichromat_2.0-0.1    farver_2.1.2         htmltools_0.5.8.1   
#> [61] labeling_0.4.3       rmarkdown_2.30       svglite_2.2.1       
#> [64] compiler_4.5.0       S7_0.2.0

References

O’Quigley, John, Margaret Pepe, and Lloyd Fisher. 1990. “Continual Reassessment Method: A Practical Design for Phase 1 Clinical Trials in Cancer.” Biometrics 46 (1): 33–48.