A mixed model of repeated measures (MMRM) analyzes longitudinal clinical trial data. In a longitudinal dataset, there are multiple patients, and each patient has multiple observations at a common set of discrete points in time.
Raw data
To use the brms.mmrm package, begin with a longitudinal
dataset with one row per patient observation and columns for the
response variable, treatment group indicator, discrete time point
indicator, patient ID variable, and optional baseline covariates such as
age and gender. As an example, consider the fev_dat dataset
from the mmrm package.
data(fev_data, package = "mmrm")It is an artificial (simulated) dataset of a clinical trial
investigating the effect of an active treatment on FEV1
(forced expired volume in one second), compared to placebo.
FEV1 is a measure of how quickly the lungs can be emptied
and low levels may indicate chronic obstructive pulmonary disease
(COPD).
The dataset is a tibble with 800 rows and the following
notable variables:
-
USUBJID(subject ID) -
AVISIT(visit number, factor) -
VISITN(visit number, numeric) -
ARMCD(treatment,TRTorPBO) -
RACE(3-category race) -
SEX(female or male) -
FEV1_BL(FEV1 at baseline, %) -
FEV1(FEV1 at study visits) -
WEIGHT(weighting variable)
For this vignette, we derive the response variable
FEV1_CHG as the change from baseline of
FEV1.
fev_data <- fev_data |>
mutate(FEV1_CHG = FEV1 - FEV1_BL)Preprocessing
We use the brm_data() function to preprocess the raw
data and express it in a special classed data frame for
brms.mmrm. brm_data() stores arguments
outcome, group, time, etc. as
attributes which the downstream post-processing functions will
recognize.
data <- brm_data(
data = fev_data,
outcome = "FEV1_CHG",
group = "ARMCD",
time = "AVISIT",
patient = "USUBJID",
baseline = "FEV1_BL",
reference_group = "PBO",
reference_time = "VIS1",
covariates = c("RACE", "SEX")
)
data
#> # A tibble: 800 × 11
#> USUBJID AVISIT ARMCD RACE SEX FEV1_BL FEV1 WEIGHT VISITN VISITN2 FEV1_CHG
#> <fct> <fct> <fct> <fct> <fct> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
#> 1 PT2 VIS1 PBO Asian Male 45.0 NA 0.465 1 0.330 NA
#> 2 PT2 VIS2 PBO Asian Male 45.0 31.5 0.233 2 -0.820 -13.6
#> 3 PT2 VIS3 PBO Asian Male 45.0 36.9 0.360 3 0.487 -8.15
#> 4 PT2 VIS4 PBO Asian Male 45.0 48.8 0.507 4 0.738 3.78
#> 5 PT3 VIS1 PBO Black or Afric… Fema… 43.5 NA 0.682 1 0.576 NA
#> 6 PT3 VIS2 PBO Black or Afric… Fema… 43.5 36.0 0.892 2 -0.305 -7.51
#> 7 PT3 VIS3 PBO Black or Afric… Fema… 43.5 NA 0.128 3 1.51 NA
#> 8 PT3 VIS4 PBO Black or Afric… Fema… 43.5 37.2 0.222 4 0.390 -6.34
#> 9 PT5 VIS1 PBO Black or Afric… Male 43.6 32.3 0.411 1 -0.0162 -11.3
#> 10 PT5 VIS2 PBO Black or Afric… Male 43.6 NA 0.422 2 0.944 NA
#> # ℹ 790 more rows
str(attributes(data))
#> List of 11
#> $ row.names : int [1:800] 1 2 3 4 5 6 7 8 9 10 ...
#> $ names : chr [1:11] "USUBJID" "AVISIT" "ARMCD" "RACE" ...
#> $ class : chr [1:4] "brms_mmrm_data" "tbl_df" "tbl" "data.frame"
#> $ brm_outcome : chr "FEV1_CHG"
#> $ brm_baseline : chr "FEV1_BL"
#> $ brm_group : chr "ARMCD"
#> $ brm_time : chr "AVISIT"
#> $ brm_patient : chr "USUBJID"
#> $ brm_covariates : chr [1:2] "RACE" "SEX"
#> $ brm_reference_group: chr "PBO"
#> $ brm_reference_time : chr "VIS1"In addition, we convert the discrete time variable
AVISIT to an ordered factor whose levels respect the
chronological order given by the continuous time variable
VISITN.
data <- data |>
brm_data_chronologize(order = "VISITN")AVISIT has a special contrasts attribute
generated by contr.treatment() to prevent base R from
automatically assigning the default but inappropriate
contr.poly() polynomial contrasts.
str(data$AVISIT)
#> Ord.factor w/ 4 levels "VIS1"<"VIS2"<..: 1 2 3 4 1 2 3 4 1 2 ...
#> - attr(*, "contrasts")= num [1:4, 1:3] 0 1 0 0 0 0 1 0 0 0 ...
#> ..- attr(*, "dimnames")=List of 2
#> .. ..$ : chr [1:4] "VIS1" "VIS2" "VIS3" "VIS4"
#> .. ..$ : chr [1:3] "2" "3" "4"Formula
Next, choose a brms model formula for the fixed effect
and variance parameters. The brm_formula() function from
brms.mmrm makes this process easier. For example, here is a
formula that omits baseline response and interaction terms.
brm_formula(
data = data,
baseline = FALSE,
baseline_time = FALSE,
group_time = FALSE
)
#> FEV1_CHG ~ ARMCD + AVISIT + RACE + SEX + unstr(time = AVISIT, gr = USUBJID)
#> sigma ~ 0 + AVISITFor the purposes of our example, we choose a fully parameterized analysis of the raw response.
formula <- brm_formula(data = data)
formula
#> FEV1_CHG ~ FEV1_BL + FEV1_BL:AVISIT + ARMCD + ARMCD:AVISIT + AVISIT + RACE + SEX + unstr(time = AVISIT, gr = USUBJID)
#> sigma ~ 0 + AVISITPriors
Some analyses require informative priors, others require
non-informative ones. Please use brms to construct
a prior suitable for your analysis. The brms package has
documentation on how its default priors are constructed and how to set
your own priors.1 Once you have an R object that represents
the joint prior distribution of your model, you can pass it to the
brm_model() function described below. The
get_prior() function shows the default priors for a given
dataset and model formula.
brms::get_prior(data = data, formula = formula) |>
as.data.frame() |>
select(-any_of(c("group", "resp", "nlpar", "lb", "ub", "source")))
#> prior class coef dpar
#> 1 b
#> 2 b ARMCDTRT
#> 3 b ARMCDTRT:AVISIT2
#> 4 b ARMCDTRT:AVISIT3
#> 5 b ARMCDTRT:AVISIT4
#> 6 b AVISIT2
#> 7 b AVISIT3
#> 8 b AVISIT4
#> 9 b FEV1_BL
#> 10 b FEV1_BL:AVISIT2
#> 11 b FEV1_BL:AVISIT3
#> 12 b FEV1_BL:AVISIT4
#> 13 b RACEBlackorAfricanAmerican
#> 14 b RACEWhite
#> 15 b SEXFemale
#> 16 lkj(1) cortime
#> 17 student_t(3, 1.9, 11.8) Intercept
#> 18 b sigma
#> 19 b AVISITVIS1 sigma
#> 20 b AVISITVIS2 sigma
#> 21 b AVISITVIS3 sigma
#> 22 b AVISITVIS4 sigmaModel
To run an MMRM, use the brm_model() function. This
function calls brms::brm() behind the scenes, using the
formula and prior you set in the formula and
prior arguments.
model <- brm_model(data = data, formula = formula, refresh = 0)
#> Compiling Stan program...
#> Start samplingThe result is a brms model object with extra list
elements brms.mmrm_data and brms.mmrm_formula
to keep track of the data and formula used to fit the model.
model
#> Family: gaussian
#> Links: mu = identity; sigma = log
#> Formula: FEV1_CHG ~ FEV1_BL + FEV1_BL:AVISIT + ARMCD + ARMCD:AVISIT + AVISIT + RACE + SEX + unstr(time = AVISIT, gr = USUBJID)
#> sigma ~ 0 + AVISIT
#> Data: modeled_data (Number of observations: 537)
#> Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#> total post-warmup draws = 4000
#>
#> Correlation Structures:
#> Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> cortime(VIS1,VIS2) 0.36 0.08 0.19 0.51 1.00 5330 3117
#> cortime(VIS1,VIS3) 0.14 0.10 -0.06 0.32 1.00 5545 2626
#> cortime(VIS2,VIS3) 0.04 0.10 -0.15 0.24 1.00 5103 3078
#> cortime(VIS1,VIS4) 0.16 0.12 -0.08 0.38 1.00 5353 2866
#> cortime(VIS2,VIS4) 0.11 0.09 -0.06 0.28 1.00 6012 3087
#> cortime(VIS3,VIS4) 0.01 0.10 -0.19 0.21 1.00 4506 2771
#>
#> Regression Coefficients:
#> Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept 23.32 2.57 18.30 28.46 1.00 1595 2142
#> FEV1_BL -0.82 0.06 -0.93 -0.70 1.00 1720 2210
#> ARMCDTRT 4.04 1.07 1.97 6.20 1.00 2694 3113
#> AVISIT2 4.43 2.75 -1.15 9.82 1.00 2037 2470
#> AVISIT3 12.55 2.93 6.74 18.27 1.00 1852 2195
#> AVISIT4 15.59 4.23 7.38 23.91 1.00 2489 2521
#> RACEBlackorAfricanAmerican 1.45 0.59 0.28 2.65 1.00 5262 3112
#> RACEWhite 5.46 0.61 4.26 6.68 1.00 5172 3218
#> SEXFemale 0.38 0.51 -0.62 1.40 1.00 5881 3056
#> FEV1_BL:AVISIT2 0.01 0.06 -0.12 0.14 1.00 2069 2704
#> FEV1_BL:AVISIT3 -0.05 0.07 -0.19 0.08 1.00 1898 2215
#> FEV1_BL:AVISIT4 -0.01 0.10 -0.21 0.19 1.00 2596 2762
#> ARMCDTRT:AVISIT2 -0.06 1.15 -2.31 2.17 1.00 2894 3132
#> ARMCDTRT:AVISIT3 -1.02 1.20 -3.37 1.38 1.00 3078 3105
#> ARMCDTRT:AVISIT4 0.35 1.88 -3.30 3.93 1.00 3810 3176
#> sigma_AVISITVIS1 1.83 0.06 1.71 1.95 1.00 5127 3300
#> sigma_AVISITVIS2 1.59 0.06 1.47 1.71 1.00 5574 3239
#> sigma_AVISITVIS3 1.33 0.06 1.21 1.45 1.00 5217 3072
#> sigma_AVISITVIS4 2.28 0.06 2.16 2.41 1.00 6592 3198
#>
#> Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).
model$brms.mmrm_data
#> # A tibble: 800 × 11
#> USUBJID AVISIT ARMCD RACE SEX FEV1_BL FEV1 WEIGHT VISITN VISITN2 FEV1_CHG
#> <fct> <ord> <fct> <fct> <fct> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
#> 1 PT2 VIS1 PBO Asian Male 45.0 NA 0.465 1 0.330 NA
#> 2 PT2 VIS2 PBO Asian Male 45.0 31.5 0.233 2 -0.820 -13.6
#> 3 PT2 VIS3 PBO Asian Male 45.0 36.9 0.360 3 0.487 -8.15
#> 4 PT2 VIS4 PBO Asian Male 45.0 48.8 0.507 4 0.738 3.78
#> 5 PT3 VIS1 PBO Black or Afric… Fema… 43.5 NA 0.682 1 0.576 NA
#> 6 PT3 VIS2 PBO Black or Afric… Fema… 43.5 36.0 0.892 2 -0.305 -7.51
#> 7 PT3 VIS3 PBO Black or Afric… Fema… 43.5 NA 0.128 3 1.51 NA
#> 8 PT3 VIS4 PBO Black or Afric… Fema… 43.5 37.2 0.222 4 0.390 -6.34
#> 9 PT5 VIS1 PBO Black or Afric… Male 43.6 32.3 0.411 1 -0.0162 -11.3
#> 10 PT5 VIS2 PBO Black or Afric… Male 43.6 NA 0.422 2 0.944 NA
#> # ℹ 790 more rows
model$brms.mmrm_formula
#> FEV1_CHG ~ FEV1_BL + FEV1_BL:AVISIT + ARMCD + ARMCD:AVISIT + AVISIT + RACE + SEX + unstr(time = AVISIT, gr = USUBJID)
#> sigma ~ 0 + AVISITMarginals
Regardless of the choice of fixed effects formula,
brms.mmrm performs inference on the marginal distributions
at each treatment group and time point of the mean of the following
quantities:
- Response.
- Change from baseline. Only reported if you originally declared a
baseline time point with the
reference_timeargument ofbrm_data(). - Treatment difference. If you declared a baseline in (2), then treatment difference is calculated in terms of change from baseline. Otherwise, it is calculated in terms of raw response.
- Effect size: treatment difference divided by the residual standard deviation.
To derive posterior draws of these marginals, use the
brm_marginal_draws() function.
draws <- brm_marginal_draws(model = model)
names(draws)
#> [1] "response" "difference_time" "difference_group" "effect"
#> [5] "sigma"
draws$difference_group
#> # A draws_df: 1000 iterations, 4 chains, and 3 variables
#> TRT|VIS2 TRT|VIS3 TRT|VIS4
#> 1 0.251 -2.24 1.149
#> 2 -0.662 -1.33 -0.804
#> 3 -0.129 -1.57 2.736
#> 4 -0.370 -2.00 1.231
#> 5 -0.964 -1.91 -1.026
#> 6 -0.939 -1.15 0.258
#> 7 -0.026 -1.15 -0.047
#> 8 0.052 -1.48 1.239
#> 9 -0.929 -0.81 -0.791
#> 10 -0.437 -1.16 2.233
#> # ... with 3990 more draws
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}If you need samples from these marginals averaged across time points,
e.g. an “overall effect size”, brm_marginal_draws_average()
can average the draws above across discrete time points (either all or a
user-defined subset).
draws_average <- brm_marginal_draws_average(draws = draws, data = data)
names(draws_average)
#> [1] "response" "difference_time" "difference_group" "effect"
#> [5] "sigma"
draws_average$difference_group
#> # A draws_df: 1000 iterations, 4 chains, and 1 variables
#> TRT|average
#> 1 -0.281
#> 2 -0.932
#> 3 0.347
#> 4 -0.380
#> 5 -1.300
#> 6 -0.610
#> 7 -0.407
#> 8 -0.064
#> 9 -0.845
#> 10 0.212
#> # ... with 3990 more draws
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}The brm_marginal_summaries() function produces posterior
summaries of these marginals, and it includes the Monte Carlo standard
error (MCSE) of each estimate.
summaries <- brm_marginal_summaries(draws, level = 0.95)
summaries
#> # A tibble: 140 × 6
#> marginal statistic group time value mcse
#> <chr> <chr> <chr> <chr> <dbl> <dbl>
#> 1 difference_group lower TRT VIS2 -2.31 0.0465
#> 2 difference_group lower TRT VIS3 -3.37 0.0668
#> 3 difference_group lower TRT VIS4 -3.30 0.0688
#> 4 difference_group mean TRT VIS2 -0.0638 0.0216
#> 5 difference_group mean TRT VIS3 -1.02 0.0219
#> 6 difference_group mean TRT VIS4 0.348 0.0311
#> 7 difference_group median TRT VIS2 -0.0714 0.0249
#> 8 difference_group median TRT VIS3 -1.02 0.0252
#> 9 difference_group median TRT VIS4 0.381 0.0320
#> 10 difference_group sd TRT VIS2 1.15 0.0161
#> # ℹ 130 more rowsThe brm_marginal_probabilities() function shows
posterior probabilities of the form,
or
brm_marginal_probabilities(
draws = draws,
threshold = c(-0.1, 0.1),
direction = c("greater", "less")
)
#> # A tibble: 6 × 5
#> direction threshold group time value
#> <chr> <dbl> <chr> <chr> <dbl>
#> 1 greater -0.1 TRT VIS2 0.511
#> 2 greater -0.1 TRT VIS3 0.220
#> 3 greater -0.1 TRT VIS4 0.594
#> 4 less 0.1 TRT VIS2 0.56
#> 5 less 0.1 TRT VIS3 0.827
#> 6 less 0.1 TRT VIS4 0.443Finally, brm_marignal_data() computes marginal means and
confidence intervals on the response variable in the data, along with
other summary statistics.
summaries_data <- brm_marginal_data(data = data, level = 0.95)
summaries_data
#> # A tibble: 56 × 4
#> statistic group time value
#> <chr> <fct> <ord> <dbl>
#> 1 lower PBO VIS1 -5.86
#> 2 lower PBO VIS2 -1.44
#> 3 lower PBO VIS3 4.33
#> 4 lower PBO VIS4 11.1
#> 5 lower TRT VIS1 0.423
#> 6 lower TRT VIS2 3.96
#> 7 lower TRT VIS3 7.67
#> 8 lower TRT VIS4 16.0
#> 9 mean PBO VIS1 -8.09
#> 10 mean PBO VIS2 -3.38
#> # ℹ 46 more rowsVisualization
Comparing models and data
Suppose we fit a second model which omits baseline.
summaries_no_baseline <- data |>
brm_formula(baseline = FALSE, baseline_time = FALSE) |>
brm_model(data = data, refresh = 0) |>
brm_marginal_draws() |>
brm_marginal_summaries()
#> Compiling Stan program...
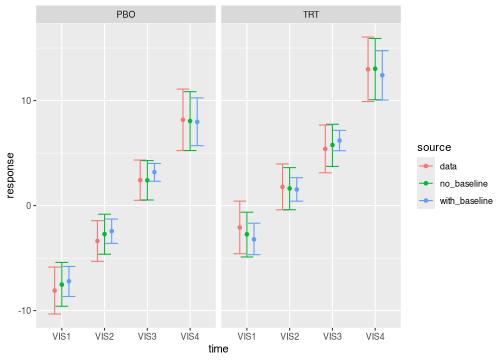
#> Start samplingThe brm_plot_compare() function compares means and
intervals from different models and data sources in the same plot.
brm_plot_compare(
data = summaries_data,
no_baseline = summaries_no_baseline,
with_baseline = summaries
)
If you omit the marginals of the data, you can show inference on change from baseline or the treatment effect.
brm_plot_compare(
no_baseline = summaries_no_baseline,
with_baseline = summaries,
marginal = "difference_group" # treatment effect
)
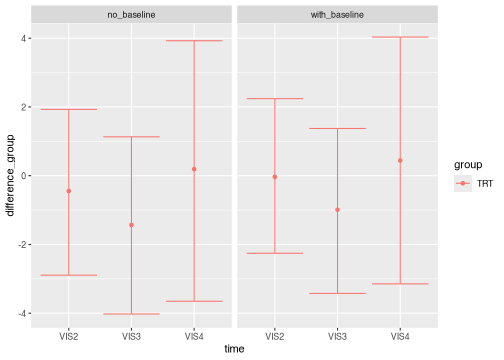
Additional arguments let you control the primary comparison of interest (the color aesthetic), the horizontal axis, and the faceting variable.
brm_plot_compare(
no_baseline = summaries_no_baseline,
with_baseline = summaries,
marginal = "difference_group",
compare = "group",
axis = "time",
facet = "source" # model1 vs model2
)
Plotting draws
brm_plot_draws() can plot the posterior draws of the
response, change from baseline, or treatment difference.
brm_plot_draws(draws = draws$difference_group)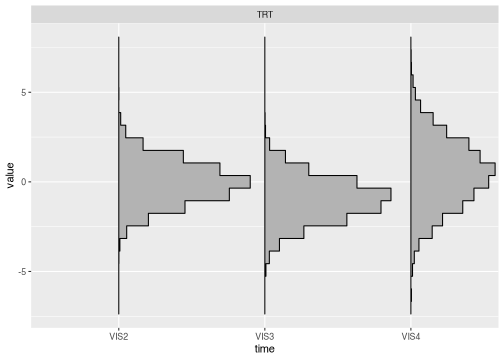
The axis and facet arguments customize the
horizontal axis and faceting variable, respectively.
brm_plot_draws(
draws = draws$difference_group,
axis = "group",
facet = "time"
)
Comparing priors and posteriors
For a model with an intercept term and with automatic centering in
brms turned on, brms by default assigns a
mildly informative Student t prior to help the MCMC converge.2
brms::prior_summary(model) |>
filter(class == "Intercept")
#> Intercept ~ student_t(3, 1.9, 11.8)Suppose we want to compare the prior on Intercept to its
marginal posterior. To begin, we express the prior using the
distributional package, extract posterior samples from the
brms model, and visualize them together with the
ggdist package. Below, the shaded gray region is the
posterior density, and the blue line is the prior density.
library(distributional)
library(ggdist)
library(ggplot2)
library(posterior)
prior <- dist_student_t(3, 1.9, 11.8)
posterior <- as_draws_df(model)
ggplot() +
stat_halfeye(aes(x = Intercept), data = posterior) +
stat_slab(aes(xdist = prior), color = "blue", fill = NA) +
scale_thickness_shared()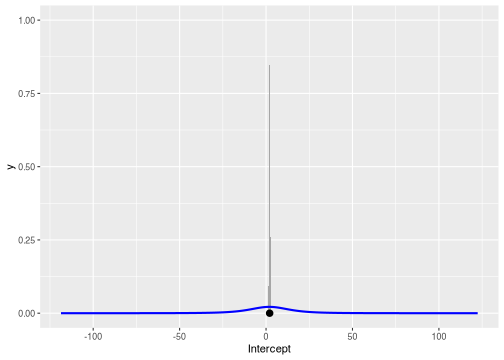
Appendix A: Contrasts
The formula is not the only factor that ultimately determines the
fixed effect parameterization. The ordering of the categorical variables
in the data, as well as the contrast option in R, affect
the construction of the model matrix. To see the model matrix that will
ultimately be used in brm_model(), run
brms::make_standata() and examine the X
element of the returned list.
The contrast option accepts a named vector of two
character vectors which govern model.matrix() contrasts for
unordered and ordered variables, respectively.
The make_standata() function lets you see the data that
brms will generate for Stan. This includes the fixed
effects model matrix X. Note the differences in the
groupgroup_* additive terms between the matrix below and
the one above.
head(brms::make_standata(formula = formula, data = data)$X)
#> Intercept FEV1_BL ARMCDPBO AVISIT2 AVISIT3 AVISIT4 RACEAsian
#> 422 1 25.27144 0 1 0 0 0
#> 424 1 25.27144 0 0 0 1 0
#> 2 1 45.02477 1 1 0 0 1
#> 3 1 45.02477 1 0 1 0 1
#> 4 1 45.02477 1 0 0 1 1
#> 6 1 43.50070 1 1 0 0 0
#> RACEBlackorAfricanAmerican SEXMale FEV1_BL:AVISIT2 FEV1_BL:AVISIT3 FEV1_BL:AVISIT4
#> 422 1 0 25.27144 0.00000 0.00000
#> 424 1 0 0.00000 0.00000 25.27144
#> 2 0 1 45.02477 0.00000 0.00000
#> 3 0 1 0.00000 45.02477 0.00000
#> 4 0 1 0.00000 0.00000 45.02477
#> 6 1 0 43.50070 0.00000 0.00000
#> ARMCDPBO:AVISIT2 ARMCDPBO:AVISIT3 ARMCDPBO:AVISIT4
#> 422 0 0 0
#> 424 0 0 0
#> 2 1 0 0
#> 3 0 1 0
#> 4 0 0 1
#> 6 1 0 0If you choose a different contrast method, a different model matrix may result.
options(
contrasts = c(unordered = "contr.treatment", ordered = "contr.poly")
)
# different model matrix than before:
head(brms::make_standata(formula = formula, data = data)$X)
#> Intercept FEV1_BL ARMCDTRT AVISIT2 AVISIT3 AVISIT4 RACEBlackorAfricanAmerican
#> 422 1 25.27144 1 1 0 0 1
#> 424 1 25.27144 1 0 0 1 1
#> 2 1 45.02477 0 1 0 0 0
#> 3 1 45.02477 0 0 1 0 0
#> 4 1 45.02477 0 0 0 1 0
#> 6 1 43.50070 0 1 0 0 1
#> RACEWhite SEXFemale FEV1_BL:AVISIT2 FEV1_BL:AVISIT3 FEV1_BL:AVISIT4 ARMCDTRT:AVISIT2
#> 422 0 1 25.27144 0.00000 0.00000 1
#> 424 0 1 0.00000 0.00000 25.27144 0
#> 2 0 0 45.02477 0.00000 0.00000 0
#> 3 0 0 0.00000 45.02477 0.00000 0
#> 4 0 0 0.00000 0.00000 45.02477 0
#> 6 0 1 43.50070 0.00000 0.00000 0
#> ARMCDTRT:AVISIT3 ARMCDTRT:AVISIT4
#> 422 0 0
#> 424 0 1
#> 2 0 0
#> 3 0 0
#> 4 0 0
#> 6 0 0Recall from earlier that brm_data_chronologize()
protects the discrete time variable (in our case, AVISIT)
from the contrasts option by assigning a
contrasts attribute of its own.
str(data$AVISIT)
#> Ord.factor w/ 4 levels "VIS1"<"VIS2"<..: 1 2 3 4 1 2 3 4 1 2 ...
#> - attr(*, "contrasts")= num [1:4, 1:3] 0 1 0 0 0 0 1 0 0 0 ...
#> ..- attr(*, "dimnames")=List of 2
#> .. ..$ : chr [1:4] "VIS1" "VIS2" "VIS3" "VIS4"
#> .. ..$ : chr [1:3] "2" "3" "4"Appendix B: Imputation of missing outcomes
Under the missing at random (MAR) assumptions, MMRMs do not require
imputation (Holzhauer and Weber (2024)).
However, if the outcomes in your data are not missing at random, or if
you are targeting an alternative estimand, then you may need to impute
missing outcomes. brms.mmrm can leverage either of the two
alternative solutions described at https://paulbuerkner.com/brms/articles/brms_missings.html.
Imputation before model fitting
To impute missing outcomes before model fitting, first use create a
list of imputed datasets using the multiple imputation method of your
choice. The rbmi
package is uniquely suited to the multiple imputation of continuous
longitudinal clinical trial data.
variables <- rbmi::set_vars(
outcome = "FEV1_CHG",
visit = "AVISIT",
subjid = "USUBJID",
group = "ARMCD",
covariates = c("RACE", "SEX")
)
imputation_draws <- rbmi::draws(
data = data |>
mutate(
USUBJID = as.factor(USUBJID),
AVISIT = as.factor(AVISIT)
),
vars = variables,
method = rbmi::method_condmean(type = "jackknife"),
quiet = TRUE
)
imputation_run <- rbmi::impute(
draws = imputation_draws,
references = c(
placebo = "PBO",
treatment = "TRT"
)
)
imputed_datasets <- rbmi::extract_imputed_dfs(imputation_run)At this point, imputed_datasets is a list of data frames
with the response variable imputed with multiple imputation. Simply
supply this list to the imputed argument of
brm_model(). Internally, brm_model() calls
brms::brm_multiple(data = imputed, formula = formula)
instead of brms::brm(data = data, formula = formula) to fit
an MMRM to each of the individual imputed datasets in the
imputed object. The computation could take several hours
because it requires many fitted MMRM.
model <- brm_model(
data = data, # Yes, please supply the original non-imputed dataset too.
formula = formula,
imputed = imputed_datasets,
refresh = 0
)Unless you set combine = FALSE in
brm_model(), brms automatically combines
posterior samples across imputed datasets. This means the downstream
post-processing workflow below is exactly the same as the non-imputation
case.
Imputation during model fitting
Alternatively, to conduct imputation during the fitting of that
model, set model_missing_outcomes to TRUE in
brm_formula(). This formula uses
response | mi() instead of just response on
the left-hand side to tell brms to model each missing
outcome as a model parameter. To use this type of imputation, simply
supply the returned formula object to the formula argument
of brm_model().
brm_formula(data, model_missing_outcomes = TRUE)
#> FEV1_CHG | mi() ~ FEV1_BL + FEV1_BL:AVISIT + ARMCD + ARMCD:AVISIT + AVISIT + RACE + SEX + unstr(time = AVISIT, gr = USUBJID)
#> sigma ~ 0 + AVISITUnlike imputation before model fitting, this approach requires only one fit of the model. However, that model will sample posterior draws for each missing outcome as if it were a model parameter, so the MCMC may run slower and produce a larger output object.