Informative prior archetypes allow users to conveniently set
informative priors in brms.mmrm in a robust way, guarding
against common pitfalls such as reference level issues, interpretation
problems, and rank deficiency.
Constructing an archetype
We begin with the FEV dataset from the mmrm package, an
artificial (simulated) dataset of a clinical trial investigating the
effect of an active treatment on FEV1 (forced expired volume in one
second), compared to placebo. FEV1 is a measure of how quickly the lungs
can be emptied and low levels may indicate chronic obstructive pulmonary
disease (COPD).
The dataset is a tibble with 800 rows and 7 variables:
-
USUBJID(subject ID), -
AVISIT(visit number), -
ARMCD(treatment, TRT or PBO), -
RACE(3-category race), -
SEX(sex), -
FEV1_BL(FEV1 at baseline, %), -
FEV1(FEV1 at study visits), -
WEIGHT(weighting variable).
library(brms.mmrm)
data(fev_data, package = "mmrm")
data <- fev_data |>
brm_data(
outcome = "FEV1",
group = "ARMCD",
time = "AVISIT",
patient = "USUBJID",
reference_time = "VIS1",
reference_group = "PBO",
covariates = c("WEIGHT", "SEX")
) |>
brm_data_chronologize(order = "VISITN")
data
#> # A tibble: 800 × 10
#> USUBJID AVISIT ARMCD RACE SEX FEV1_BL FEV1 WEIGHT VISITN VISITN2
#> <fct> <ord> <fct> <fct> <fct> <dbl> <dbl> <dbl> <int> <dbl>
#> 1 PT2 VIS1 PBO Asian Male 45.0 NA 0.465 1 0.330
#> 2 PT2 VIS2 PBO Asian Male 45.0 31.5 0.233 2 -0.820
#> 3 PT2 VIS3 PBO Asian Male 45.0 36.9 0.360 3 0.487
#> 4 PT2 VIS4 PBO Asian Male 45.0 48.8 0.507 4 0.738
#> 5 PT3 VIS1 PBO Black or African A… Fema… 43.5 NA 0.682 1 0.576
#> 6 PT3 VIS2 PBO Black or African A… Fema… 43.5 36.0 0.892 2 -0.305
#> 7 PT3 VIS3 PBO Black or African A… Fema… 43.5 NA 0.128 3 1.51
#> 8 PT3 VIS4 PBO Black or African A… Fema… 43.5 37.2 0.222 4 0.390
#> 9 PT5 VIS1 PBO Black or African A… Male 43.6 32.3 0.411 1 -0.0162
#> 10 PT5 VIS2 PBO Black or African A… Male 43.6 NA 0.422 2 0.944
#> # ℹ 790 more rowsThe functions listed at https://openpharma.github.io/brms.mmrm/reference/index.html#informative-prior-archetypes can create different kinds of informative prior archetypes from a dataset like the one above. For example, suppose we want to place informative priors on the successive differences between adjacent time points. This approach is appropriate and desirable in many situations because the structure naturally captures the prior correlations among adjacent visits of a clinical trial. To do this, we create an instance of the “successive cells” archetype.
archetype <- brm_archetype_successive_cells(data, baseline = FALSE)The instance of the archetype is an ordinary tibble, but it adds new
columns with prefixes "x_" and "nuisance_".
These new columns constitute a custom model matrix to describe the
desired parameterization.
archetype
#> # A tibble: 800 × 20
#> x_PBO_VIS1 x_PBO_VIS2 x_PBO_VIS3 x_PBO_VIS4 x_TRT_VIS1 x_TRT_VIS2 x_TRT_VIS3
#> * <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 0 0 0 0 0 0
#> 2 1 1 0 0 0 0 0
#> 3 1 1 1 0 0 0 0
#> 4 1 1 1 1 0 0 0
#> 5 1 0 0 0 0 0 0
#> 6 1 1 0 0 0 0 0
#> 7 1 1 1 0 0 0 0
#> 8 1 1 1 1 0 0 0
#> 9 1 0 0 0 0 0 0
#> 10 1 1 0 0 0 0 0
#> # ℹ 790 more rows
#> # ℹ 13 more variables: x_TRT_VIS4 <dbl>, nuisance_WEIGHT <dbl>,
#> # nuisance_SEX_Male <dbl>, USUBJID <fct>, AVISIT <ord>, ARMCD <fct>, RACE <fct>,
#> # SEX <fct>, FEV1_BL <dbl>, FEV1 <dbl>, WEIGHT <dbl>, VISITN <int>, VISITN2 <dbl>We have effects of interest to express successive differences:
attr(archetype, "brm_archetype_interest")
#> [1] "x_PBO_VIS1" "x_PBO_VIS2" "x_PBO_VIS3" "x_PBO_VIS4" "x_TRT_VIS1" "x_TRT_VIS2"
#> [7] "x_TRT_VIS3" "x_TRT_VIS4"We also have nuisance variables. Some nuisance variables are
continuous covariates, while others are levels of one-hot-encoded
concomitant factors or interactions of those concomitant factors with
baseline and/or subgroup. All nuisance variables are centered at their
means so the reference level of the model is at the “center” of the data
and not implicitly conditional on a subset of the data.1 In addition, some
nuisance variables are automatically dropped in order to ensure the
model matrix is full-rank, and automatic centering in brms
is disabled2. This is critically important to preserve
the interpretation of the columns of interest and make sure the
informative priors behave as expected.
attr(archetype, "brm_archetype_nuisance")
#> [1] "nuisance_WEIGHT" "nuisance_SEX_Male"The factors of interest linearly map to marginal means. To see the
mapping, call summary() on the archetype. The printed
output helps build intuition on how the archetype is parameterized and
what those parameters are doing.3
summary(archetype)
#> # This is the "successive cells" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS1 + x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3 + x_PBO_VIS4
#> # TRT:VIS1 = x_TRT_VIS1
#> # TRT:VIS2 = x_TRT_VIS1 + x_TRT_VIS2
#> # TRT:VIS3 = x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3
#> # TRT:VIS4 = x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3 + x_TRT_VIS4Above, x_PBO_VIS1 serves as the intercept, and
x_TRT_VIS1 is defined relative to x_TRT_VIS1.
The rest of the parameters keep their original interpretations.
Informative priors
Let’s assume you want to assign informative priors to the fixed
effect parameters of interest declared in the archetype, such as
x_group_1_time_2 and x_group_2_time_3. Your
priors may come from expert elicitation, historical data, or some other
method, and you might consider distributional
families recommended by the Stan team. However you construct these
priors, brms.mmrm helps you assign them to the model
without having to guess at the automatically-generated names of model
coefficients in R.
In the printed output from summary(archetype),
parameters of interest such as x_group_1_time_2 and
x_group_2_time_3 are always labeled using treatment groups
and time points in the data (and subgroup levels, if applicable). This
labeling mechanism is the same regardless of which archetype you choose,
and it the way brms.mmrm helps you assign priors.
brm_prior_label() is one way to create a labeling
scheme. Each call to brm_prior_label() below assigns a
univariate prior to a fixed effect parameter. Each univariate prior is a
Stan code string. Possible choices are documented in the Stan function
reference at https://mc-stan.org/docs/functions-reference/unbounded_continuous_distributions.html.
label <- NULL |>
brm_prior_label(code = "student_t(4, -7.57, 4.96)", group = "PBO", time = "VIS1") |>
brm_prior_label(code = "student_t(4, 3.14, 7.86)", group = "PBO", time = "VIS2") |>
brm_prior_label(code = "student_t(4, 8.78, 8.18)", group = "PBO", time = "VIS3") |>
brm_prior_label(code = "student_t(4, 3.36, 8.10)", group = "PBO", time = "VIS4") |>
brm_prior_label(code = "student_t(4, -2.96, 4.78)", group = "TRT", time = "VIS1") |>
brm_prior_label(code = "student_t(4, 3.13, 7.64)", group = "TRT", time = "VIS2") |>
brm_prior_label(code = "student_t(4, 7.65, 8.24)", group = "TRT", time = "VIS3") |>
brm_prior_label(code = "student_t(4, 4.64, 8.21)", group = "TRT", time = "VIS4")
label
#> # A tibble: 8 × 3
#> code group time
#> <chr> <chr> <chr>
#> 1 student_t(4, -7.57, 4.96) PBO VIS1
#> 2 student_t(4, 3.14, 7.86) PBO VIS2
#> 3 student_t(4, 8.78, 8.18) PBO VIS3
#> 4 student_t(4, 3.36, 8.10) PBO VIS4
#> 5 student_t(4, -2.96, 4.78) TRT VIS1
#> 6 student_t(4, 3.13, 7.64) TRT VIS2
#> 7 student_t(4, 7.65, 8.24) TRT VIS3
#> 8 student_t(4, 4.64, 8.21) TRT VIS4As an alternative to brm_prior_label(), you can start
with a template and manually fill in the Stan code.
template <- brm_prior_template(archetype)
template
#> # A tibble: 8 × 3
#> code group time
#> <chr> <chr> <chr>
#> 1 <NA> PBO VIS1
#> 2 <NA> PBO VIS2
#> 3 <NA> PBO VIS3
#> 4 <NA> PBO VIS4
#> 5 <NA> TRT VIS1
#> 6 <NA> TRT VIS2
#> 7 <NA> TRT VIS3
#> 8 <NA> TRT VIS4
label <- template |>
mutate(
code = c(
"student_t(4, -7.57, 4.96)",
"student_t(4, 3.14, 7.86)",
"student_t(4, 8.78, 8.18)",
"student_t(4, 3.36, 8.10)",
"student_t(4, -2.96, 4.78)",
"student_t(4, 3.13, 7.64)",
"student_t(4, 7.65, 8.24)",
"student_t(4, 4.64, 8.21)"
)
)
label
#> # A tibble: 8 × 3
#> code group time
#> <chr> <chr> <chr>
#> 1 student_t(4, -7.57, 4.96) PBO VIS1
#> 2 student_t(4, 3.14, 7.86) PBO VIS2
#> 3 student_t(4, 8.78, 8.18) PBO VIS3
#> 4 student_t(4, 3.36, 8.10) PBO VIS4
#> 5 student_t(4, -2.96, 4.78) TRT VIS1
#> 6 student_t(4, 3.13, 7.64) TRT VIS2
#> 7 student_t(4, 7.65, 8.24) TRT VIS3
#> 8 student_t(4, 4.64, 8.21) TRT VIS4After you have a labeling scheme, brm_prior_archetype()
can create a brms prior for the important fixed effects.4
prior <- brm_prior_archetype(label = label, archetype = archetype)
prior
#> prior class coef group resp dpar nlpar lb ub source
#> student_t(4, -7.57, 4.96) b x_PBO_VIS1 <NA> <NA> user
#> student_t(4, 3.14, 7.86) b x_PBO_VIS2 <NA> <NA> user
#> student_t(4, 8.78, 8.18) b x_PBO_VIS3 <NA> <NA> user
#> student_t(4, 3.36, 8.10) b x_PBO_VIS4 <NA> <NA> user
#> student_t(4, -2.96, 4.78) b x_TRT_VIS1 <NA> <NA> user
#> student_t(4, 3.13, 7.64) b x_TRT_VIS2 <NA> <NA> user
#> student_t(4, 7.65, 8.24) b x_TRT_VIS3 <NA> <NA> user
#> student_t(4, 4.64, 8.21) b x_TRT_VIS4 <NA> <NA> userIn less common situations, you may wish to assign priors to nuisance
parameters. For example, our model accounts for interactions between
baseline and discrete time, and it may be reasonable to assign priors to
these slopes based on high-quality historical data. This requires a
thorough understanding of the fixed effect structure of the model, but
it can be done directly through brms. First, check the
formula for the included nuisance parameters. brm_formula()
automatically understands archetypes.
brm_formula(archetype)
#> FEV1 ~ 0 + x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3 + x_PBO_VIS4 + x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3 + x_TRT_VIS4 + nuisance_WEIGHT + nuisance_SEX_Male + unstr(time = AVISIT, gr = USUBJID)
#> sigma ~ 0 + AVISITThe "nuisance_*" terms are the nuisance variables, and
the ones involving baseline are
nuisance_FEV1_BL.AVISITVIS1,
nuisance_FEV1_BL.AVISITVIS2,
nuisance_FEV1_BL.AVISITVIS3, and
nuisance_FEV1_BL.AVISITVIS4. Because there is no overall
slope for baseline, we can interpret each term as the linear rate of
change in the outcome variable per unit increase in baseline for a given
discrete time point. Suppose we use this interpretation to construct
informative priors student_t(4, -0.83, 1),
student_t(4, -0.78, 1),
student_t(4, -0.86, 1), and
student_t(4, -0.82, 1), respectively. Use
brms::set_prior() and c() to append these
priors to our existing prior object:
The model still has many parameters where we did not set priors, and
brms sets automatic defaults. You can see these defaults
with brms::get_prior().
https://paulbuerkner.com/brms/reference/set_prior.html
documents many of the default priors set by brms. In
particular, "(flat)" denotes an improper uniform prior over
all the real numbers.
Modeling and analysis
The downstream methods in brms.mmrm automatically
understand how to work with informative prior archetypes. Notably, the
formula uses custom interest and nuisance variables instead of the
original variables in the data.
formula <- brm_formula(archetype)
formula
#> FEV1 ~ 0 + x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3 + x_PBO_VIS4 + x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3 + x_TRT_VIS4 + nuisance_WEIGHT + nuisance_SEX_Male + unstr(time = AVISIT, gr = USUBJID)
#> sigma ~ 0 + AVISITThe model can accept the archetype, formula, and prior. Usage is the same as in non-archetype workflows.
model <- brm_model(
data = archetype,
formula = formula,
prior = prior,
refresh = 0
)
#> Compiling Stan program...
#> Start sampling
brms::prior_summary(model)
#> prior class coef group resp dpar nlpar lb ub
#> (flat) b
#> (flat) b nuisance_SEX_Male
#> (flat) b nuisance_WEIGHT
#> student_t(4, -7.57, 4.96) b x_PBO_VIS1
#> student_t(4, 3.14, 7.86) b x_PBO_VIS2
#> student_t(4, 8.78, 8.18) b x_PBO_VIS3
#> student_t(4, 3.36, 8.10) b x_PBO_VIS4
#> student_t(4, -2.96, 4.78) b x_TRT_VIS1
#> student_t(4, 3.13, 7.64) b x_TRT_VIS2
#> student_t(4, 7.65, 8.24) b x_TRT_VIS3
#> student_t(4, 4.64, 8.21) b x_TRT_VIS4
#> (flat) b sigma
#> (flat) b AVISITVIS1 sigma
#> (flat) b AVISITVIS2 sigma
#> (flat) b AVISITVIS3 sigma
#> (flat) b AVISITVIS4 sigma
#> lkj_corr_cholesky(1) Lcortime
#> source
#> default
#> (vectorized)
#> (vectorized)
#> user
#> user
#> user
#> user
#> user
#> user
#> user
#> user
#> default
#> (vectorized)
#> (vectorized)
#> (vectorized)
#> (vectorized)
#> defaultMarginal mean estimation, post-processing, and visualization automatically understand the archetype without any user intervention.
draws <- brm_marginal_draws(
data = archetype,
formula = formula,
model = model
)
summaries_model <- brm_marginal_summaries(draws)
summaries_data <- brm_marginal_data(archetype)
brm_plot_compare(model = summaries_model, data = summaries_data)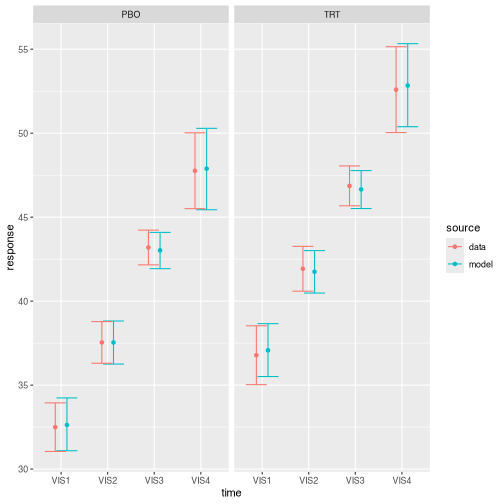
plot of chunk archetype_compare_data
All archetypes
brms.mmrm supports a variety of informative prior
archetypes with different kinds of fixed effects. For example,
brms.mmrm supports simple cell mean and treatment effect
parameterizations.
summary(brm_archetype_cells(data, intercept = FALSE))
#> # This is the "cells" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS4
#> # TRT:VIS1 = x_TRT_VIS1
#> # TRT:VIS2 = x_TRT_VIS2
#> # TRT:VIS3 = x_TRT_VIS3
#> # TRT:VIS4 = x_TRT_VIS4
summary(brm_archetype_effects(data, intercept = FALSE))
#> # This is the "effects" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS4
#> # TRT:VIS1 = x_PBO_VIS1 + x_TRT_VIS1
#> # TRT:VIS2 = x_PBO_VIS2 + x_TRT_VIS2
#> # TRT:VIS3 = x_PBO_VIS3 + x_TRT_VIS3
#> # TRT:VIS4 = x_PBO_VIS4 + x_TRT_VIS4There are archetypes to parameterize the average across all time
points in the data. Below, x_group_1_time_2 is the average
across time points for group 1 because it is the algebraic result of
simplifying
(group_1:time_2 + group_1:time_3 + group_1:time_3) / 3.
summary(brm_archetype_average_cells(data, intercept = FALSE))
#> # This is the "average cells" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = 4*x_PBO_VIS1 - x_PBO_VIS2 - x_PBO_VIS3 - x_PBO_VIS4
#> # PBO:VIS2 = x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS4
#> # TRT:VIS1 = 4*x_TRT_VIS1 - x_TRT_VIS2 - x_TRT_VIS3 - x_TRT_VIS4
#> # TRT:VIS2 = x_TRT_VIS2
#> # TRT:VIS3 = x_TRT_VIS3
#> # TRT:VIS4 = x_TRT_VIS4There is also a treatment effect version where
x_group_2_time_2 becomes the time-averaged treatment effect
of group 2 relative to group 1.
summary(brm_archetype_average_effects(data, intercept = FALSE))
#> # This is the "average effects" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = 4*x_PBO_VIS1 - x_PBO_VIS2 - x_PBO_VIS3 - x_PBO_VIS4
#> # PBO:VIS2 = x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS4
#> # TRT:VIS1 = 4*x_PBO_VIS1 - x_PBO_VIS2 - x_PBO_VIS3 - x_PBO_VIS4 + 4*x_TRT_VIS1 - x_TRT_VIS2 - x_TRT_VIS3 - x_TRT_VIS4
#> # TRT:VIS2 = x_PBO_VIS2 + x_TRT_VIS2
#> # TRT:VIS3 = x_PBO_VIS3 + x_TRT_VIS3
#> # TRT:VIS4 = x_PBO_VIS4 + x_TRT_VIS4The example in this vignette uses the “successive cells” archetype, where fixed effects represent successive differences between adjacent time points.
summary(brm_archetype_successive_cells(data, intercept = FALSE))
#> # This is the "successive cells" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS1 + x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3 + x_PBO_VIS4
#> # TRT:VIS1 = x_TRT_VIS1
#> # TRT:VIS2 = x_TRT_VIS1 + x_TRT_VIS2
#> # TRT:VIS3 = x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3
#> # TRT:VIS4 = x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3 + x_TRT_VIS4There is also a treatment effect version of the successive differences archetype:
summary(brm_archetype_successive_effects(data, intercept = FALSE))
#> # This is the "successive effects" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS1 + x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3 + x_PBO_VIS4
#> # TRT:VIS1 = x_PBO_VIS1 + x_TRT_VIS1
#> # TRT:VIS2 = x_PBO_VIS1 + x_PBO_VIS2 + x_TRT_VIS1 + x_TRT_VIS2
#> # TRT:VIS3 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3 + x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3
#> # TRT:VIS4 = x_PBO_VIS1 + x_PBO_VIS2 + x_PBO_VIS3 + x_PBO_VIS4 + x_TRT_VIS1 + x_TRT_VIS2 + x_TRT_VIS3 + x_TRT_VIS4Variations on archetypes
Archetypes can be customized. As an example, consider the simple cell means archetype.
summary(brm_archetype_cells(data))
#> # This is the "cells" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS4
#> # TRT:VIS1 = x_TRT_VIS1
#> # TRT:VIS2 = x_TRT_VIS2
#> # TRT:VIS3 = x_TRT_VIS3
#> # TRT:VIS4 = x_TRT_VIS4To include an intercept term which all the marginal means share, set
intercept = TRUE.
summary(brm_archetype_cells(data, intercept = TRUE))
#> # This is the "cells" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS1 + x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS1 + x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS1 + x_PBO_VIS4
#> # TRT:VIS1 = x_PBO_VIS1 + x_TRT_VIS1
#> # TRT:VIS2 = x_PBO_VIS1 + x_TRT_VIS2
#> # TRT:VIS3 = x_PBO_VIS1 + x_TRT_VIS3
#> # TRT:VIS4 = x_PBO_VIS1 + x_TRT_VIS4To set up constrained longitudinal data analysis (cLDA), set
clda = TRUE. This constraint pools all treatment groups at
baseline, and it can help model clinical trials where a baseline
measurement is observed before randomization. Some archetypes cannot
support cLDA (e.g. brm_archetype_average_cells() and
brm_archetype_average_effects()).
summary(brm_archetype_cells(data, clda = TRUE))
#> # This is the "cells" informative prior archetype in brms.mmrm.
#> # The following equations show the relationships between the
#> # marginal means (left-hand side) and fixed effect parameters
#> # (right-hand side).
#> #
#> # PBO:VIS1 = x_PBO_VIS1
#> # PBO:VIS2 = x_PBO_VIS2
#> # PBO:VIS3 = x_PBO_VIS3
#> # PBO:VIS4 = x_PBO_VIS4
#> # TRT:VIS1 = x_PBO_VIS1
#> # TRT:VIS2 = x_TRT_VIS2
#> # TRT:VIS3 = x_TRT_VIS3
#> # TRT:VIS4 = x_TRT_VIS4