Plot PseudoDualFlexiSimulations
Source: R/Simulations-methods.R
plot-PseudoDualFlexiSimulations-missing-method.RdSummarize the simulations with plots.
This plot method can be applied to PseudoDualFlexiSimulations objects in
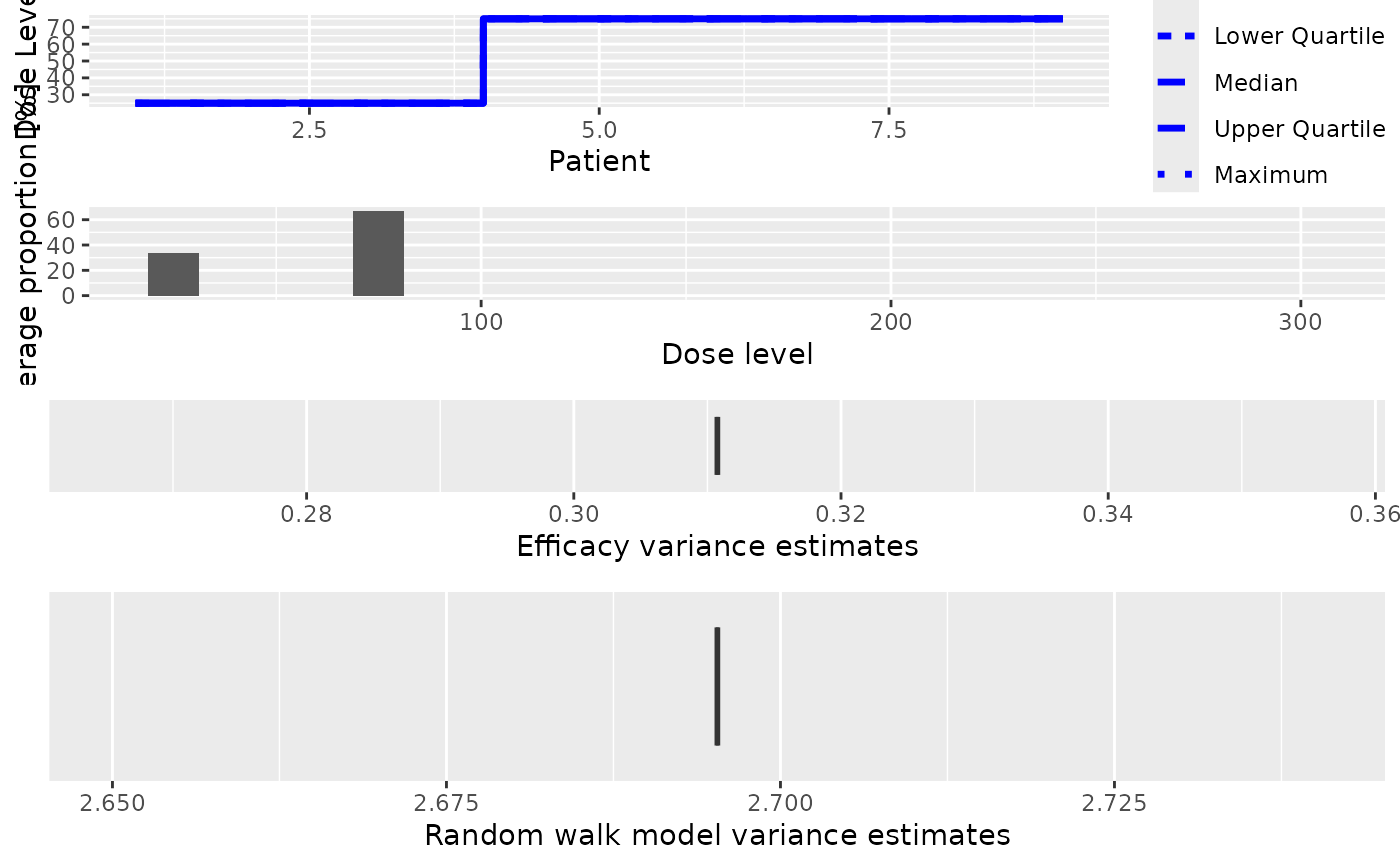
order to summarize them graphically. Possible types of plots at the moment
are:
- trajectory
Summary of the trajectory of the simulated trials
- dosesTried
Average proportions of the doses tested in patients
- sigma2
The variance of the efficacy responses
- sigma2betaW
The variance of the random walk model
You can specify one or both of these in the type argument.
Examples
# Obtain the plot for the simulation results if DLE and efficacy responses
# are considered in the simulations.
emptydata <- DataDual(doseGrid = seq(25, 300, 25))
# The DLE model must be of 'ModelTox' (e.g 'LogisticIndepBeta') class.
dle_model <- LogisticIndepBeta(
binDLE = c(1.05, 1.8),
DLEweights = c(3, 3),
DLEdose = c(25, 300),
data = emptydata
)
# The efficacy model must be of 'EffFlexi' class.
eff_model <- EffFlexi(
eff = c(1.223, 2.513),
eff_dose = c(25, 300),
sigma2W = c(a = 0.1, b = 0.1),
sigma2betaW = c(a = 20, b = 50),
rw1 = FALSE,
data = emptydata
)
# The escalation rule using the 'NextBestMaxGainSamples' class.
my_next_best <- NextBestMaxGainSamples(
prob_target_drt = 0.35,
prob_target_eot = 0.3,
derive = function(samples) {
as.numeric(quantile(samples, prob = 0.3))
},
mg_derive = function(mg_samples) {
as.numeric(quantile(mg_samples, prob = 0.5))
}
)
# The cohort size, size of 3 subjects.
my_size <- CohortSizeConst(size = 3)
# Allow increase of 200%.
my_increments <- IncrementsRelative(intervals = 0, increments = 2)
# Define the stopping rule. Stop when the maximum sample size of 36 patients has
# been reached or when the next dose is NA.
my_stopping <- StoppingMinPatients(nPatients = 36) | StoppingMissingDose()
# Specify the design.
design <- DualResponsesSamplesDesign(
nextBest = my_next_best,
cohort_size = my_size,
startingDose = 25,
model = dle_model,
eff_model = eff_model,
data = emptydata,
stopping = my_stopping,
increments = my_increments
)
# Specify the true DLE curve and the true expected efficacy values
# at all dose levels.
my_truth_dle <- probFunction(dle_model, phi1 = -53.66584, phi2 = 10.50499)
my_truth_eff <- c(
-0.5478867,
0.1645417,
0.5248031,
0.7604467,
0.9333009,
1.0687031,
1.1793942,
1.2726408,
1.3529598,
1.4233411,
1.4858613,
1.5420182
)
# The true gain curve.
my_truth_gain <- function(dose) {
return((myTruthEff(dose)) / (1 + (myTruthDLE(dose) / (1 - myTruthDLE(dose)))))
}
# MCMC options.
my_options <- McmcOptions(burnin = 10, step = 1, samples = 20)
# For illustration purpose only 1 simulation is produced.
my_sim <- simulate(
object = design,
args = NULL,
trueDLE = my_truth_dle,
trueEff = my_truth_eff,
trueSigma2 = 0.025,
trueSigma2betaW = 1,
mcmcOptions = my_options,
nsim = 1,
seed = 819,
parallel = FALSE
)
# Plot the simulated results.
print(plot(my_sim))