(superseded) simaerep Portfolio Performance • simaerep

Load

suppressPackageStartupMessages(library(tidyverse))
suppressPackageStartupMessages(library(knitr))
suppressPackageStartupMessages(library(furrr))
suppressPackageStartupMessages(library(future))
suppressPackageStartupMessages(library(simaerep))

# RAM ~26 GB
# plan 4GB per core
plan(multisession, workers = 6)

Introduction

We want to define minimal requirements for simulating test data that reflects realistic portfolio data which we then want to use to benchmark overall {simaerep} performance.

Performance

These simulations take some time to run and require multiple cores and appropriate memory. Rendering articles in {pkgdown} can be a bit unstable so we recommend to render first using pure {rmarkdown} to generate the intermediate csv files.

rmarkdown::render("vignettes/_portfolio_perf.Rmd", knit_root_dir = paste0(getwd(), "/vignettes"))

Portfolio Configuration

The portfolio configuration will be used to generate compliant test data that is similar to a realistic portfolio of studies in which all sites are compliant. We will subsequently remove a percentage of AEs from each study site and calculate AE under-reporting statistics to calculate overall detection thresholds. The portfolio configuration should give a minimal description of the portfolio without violating data privacy laws or competitive intellectual property. We propose to include the following metrics into the portfolio configuration:

site parameters:

mean of all maximum patient visits
sd of of all maximum patient visits
total number patients

study parameters:

mean AE per visit

The information contained in a portfolio configuration is very scarce and thus can be shared more easily within the industry. We can use those parameters to simulate test data for assessing {simaerep} performance on a given portfolio.

We can start with a maximum aggregation of visit and n_ae on patient level starting with df_visit as we would use it for simaerep::site_aggr(). We can use simaerep::get_config to generate a valid portfolio configuration, which will automatically apply a few filters:

remove patients with 0 visits
minimum number of patients per study
minimum number of sites per study
anonymize study and site IDs

df_visit1 <- sim_test_data_study(n_pat = 100, n_sites = 10,
   frac_site_with_ur = 0.4, ur_rate = 0.6)

df_visit1$study_id <- "A"

df_visit2 <- sim_test_data_study(n_pat = 100, n_sites = 10,
                                      frac_site_with_ur = 0.2, ur_rate = 0.1)

df_visit2$study_id <- "B"

df_visit <- bind_rows(df_visit1, df_visit2)

df_site_max <- df_visit %>%
  group_by(study_id, site_number, patnum) %>%
  summarise(max_visit = max(visit),
            max_ae = max(n_ae),
            .groups = "drop")

df_config <- simaerep::get_config(
  df_site_max, anonymize = TRUE,
  min_pat_per_study = 100,
  min_sites_per_study = 10
)

df_config %>%
  head(25) %>%
  knitr::kable()

study_id	ae_per_visit_mean	site_number	max_visit_sd	max_visit_mean	n_pat
0001	0.3997929	0001	4.175324	19.1	10
0001	0.3997929	0002	5.108816	18.1	10
0001	0.3997929	0003	3.011091	18.8	10
0001	0.3997929	0004	3.366502	18.0	10
0001	0.3997929	0005	3.831159	18.7	10
0001	0.3997929	0006	2.708013	19.0	10
0001	0.3997929	0007	1.885618	20.0	10
0001	0.3997929	0008	3.333333	20.0	10
0001	0.3997929	0009	3.765339	22.2	10
0001	0.3997929	0010	2.898275	19.2	10
0002	0.4793602	0001	4.237400	17.8	10
0002	0.4793602	0002	3.622461	19.3	10
0002	0.4793602	0003	3.272783	18.6	10
0002	0.4793602	0004	4.648775	20.5	10
0002	0.4793602	0005	3.368152	20.3	10
0002	0.4793602	0006	4.083844	20.3	10
0002	0.4793602	0007	4.900113	19.3	10
0002	0.4793602	0008	3.622461	20.3	10
0002	0.4793602	0009	3.604010	17.9	10
0002	0.4793602	0010	3.308239	19.5	10

Simulate Portfolio from Configuration

We can now apply sim_test_data_portfolio which uses sim_test_data_study() to generate artificial data on visit level.

df_portf <- sim_test_data_portfolio(df_config)

df_portf %>%
  head(25) %>%
  knitr::kable()

study_id	ae_per_visit_mean	site_number	max_visit_sd	max_visit_mean	patnum	visit	n_ae
0001	0.3997929	0001	4.175324	19.1	0001	1	1
0001	0.3997929	0001	4.175324	19.1	0001	2	1
0001	0.3997929	0001	4.175324	19.1	0001	3	2
0001	0.3997929	0001	4.175324	19.1	0001	4	2
0001	0.3997929	0001	4.175324	19.1	0001	5	2
0001	0.3997929	0001	4.175324	19.1	0001	6	2
0001	0.3997929	0001	4.175324	19.1	0001	7	2
0001	0.3997929	0001	4.175324	19.1	0001	8	2
0001	0.3997929	0001	4.175324	19.1	0001	9	2
0001	0.3997929	0001	4.175324	19.1	0001	10	2
0001	0.3997929	0001	4.175324	19.1	0001	11	3
0001	0.3997929	0001	4.175324	19.1	0001	12	3
0001	0.3997929	0001	4.175324	19.1	0001	13	4
0001	0.3997929	0001	4.175324	19.1	0001	14	4
0001	0.3997929	0001	4.175324	19.1	0001	15	5
0001	0.3997929	0001	4.175324	19.1	0001	16	6
0001	0.3997929	0001	4.175324	19.1	0001	17	7
0001	0.3997929	0001	4.175324	19.1	0001	18	7
0001	0.3997929	0001	4.175324	19.1	0002	1	1
0001	0.3997929	0001	4.175324	19.1	0002	2	1
0001	0.3997929	0001	4.175324	19.1	0002	3	1
0001	0.3997929	0001	4.175324	19.1	0002	4	2
0001	0.3997929	0001	4.175324	19.1	0002	5	2
0001	0.3997929	0001	4.175324	19.1	0002	6	2
0001	0.3997929	0001	4.175324	19.1	0002	7	3

Load Realistic Configuration

Here we load a realistic portfolio configuration.

df_config <- readr::read_csv("ae_profile.csv")

df_config %>%
  head(25) %>%
  knitr::kable()

study_id	ae_per_visit_mean	ae_per_day_mean	site_number	max_visit_sd	max_visit_mean	max_days_sd	max_days_mean	n_pat
0001	0.2687087	0.0072492	0001	0.7071068	22.50000	622	622	2
0001	0.2687087	0.0072492	0002	2.1213203	28.50000	1350	1350	2
0001	0.2687087	0.0072492	0003	0.5773503	19.50000	738	738	4
0001	0.2687087	0.0072492	0004	8.8694231	31.33333	1461	1461	6
0001	0.2687087	0.0072492	0005	0.0000000	30.00000	1253	1253	1
0001	0.2687087	0.0072492	0006	0.0000000	35.00000	1479	1479	1
0001	0.2687087	0.0072492	0007	0.0000000	36.00000	1415	1415	1
0001	0.2687087	0.0072492	0008	5.3363087	26.14286	971	971	7
0001	0.2687087	0.0072492	0009	0.0000000	20.00000	756	756	2
0001	0.2687087	0.0072492	0010	1.8165902	27.40000	1364	1364	5
0001	0.2687087	0.0072492	0011	1.7320508	27.00000	1190	1190	3
0001	0.2687087	0.0072492	0012	1.4142136	26.00000	1186	1186	2
0001	0.2687087	0.0072492	0013	0.0000000	25.00000	1127	1127	1
0001	0.2687087	0.0072492	0014	0.0000000	18.00000	566	566	1
0001	0.2687087	0.0072492	0015	1.7078251	18.75000	588	588	4
0001	0.2687087	0.0072492	0016	0.0000000	25.00000	644	644	1
0001	0.2687087	0.0072492	0017	1.0000000	22.00000	827	827	3
0001	0.2687087	0.0072492	0018	4.0414519	32.50000	1534	1534	4
0001	0.2687087	0.0072492	0019	12.9408913	25.33333	1183	1183	6
0001	0.2687087	0.0072492	0020	0.5773503	20.66667	770	770	3
0001	0.2687087	0.0072492	0021	14.8492424	28.50000	666	666	2
0001	0.2687087	0.0072492	0022	9.0369611	26.50000	987	987	4
0001	0.2687087	0.0072492	0023	0.0000000	23.00000	931	931	1
0001	0.2687087	0.0072492	0024	0.0000000	38.00000	938	938	1
0001	0.2687087	0.0072492	0025	6.3639610	26.50000	938	938	2

Simulate Portfolio

And again we simulate artificial visit level data. Using parallel processing. At this stage we have simulated compliant test data of a realistic study portfolio.

df_portf <- sim_test_data_portfolio(df_config, parallel = TRUE, progress = TRUE)

df_portf %>%
  head(25) %>%
  knitr::kable()

study_id	ae_per_visit_mean	ae_per_day_mean	site_number	max_visit_sd	max_visit_mean	max_days_sd	max_days_mean	patnum	visit	n_ae
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	1	0
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	2	0
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	3	0
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	4	1
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	5	1
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	6	1
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	7	1
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	8	1
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	9	1
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	10	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	11	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	12	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	13	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	14	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	15	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	16	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	17	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	18	2
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	19	5
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	20	5
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	21	5
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0001	22	6
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0002	1	0
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0002	2	0
0001	0.2687087	0.0072492	0001	0.7071068	22.5	622	622	0002	3	1

Confirm that Portfolio Simulation results in Similar Configuration

We will now use the simulated portfolio data and extract the configuration. We expect that the configuration that we will be extracting is very similar to the configuration that we started out with in the first place.

df_site_max_portf <- df_portf %>%
  group_by(study_id, site_number, patnum) %>%
  summarise(max_visit = max(visit),
            max_ae = max(n_ae),
            .groups = "drop")

df_config_portf <- simaerep::get_config(df_site_max_portf, anonymize = TRUE, min_pat_per_study = 100, min_sites_per_study = 10)

df_comp <- df_config %>%
  left_join(
    df_config_portf,
    by = c("study_id", "site_number"),
    suffix = c(".ori", ".sim")
  ) %>%
  select(
    study_id,
    starts_with("ae"),
    site_number,
    contains("max_visit_sd"),
    contains("max_visit_mean"),
    contains("n_pat")
  )

df_comp %>%
  select(study_id, starts_with("ae")) %>%
  distinct() %>%
  ggplot(aes(ae_per_visit_mean.ori, ae_per_visit_mean.sim)) +
    geom_point() +
    geom_smooth() +
    labs(title = "simulated vs original AE per visit study mean") +
    theme(aspect.ratio = 1)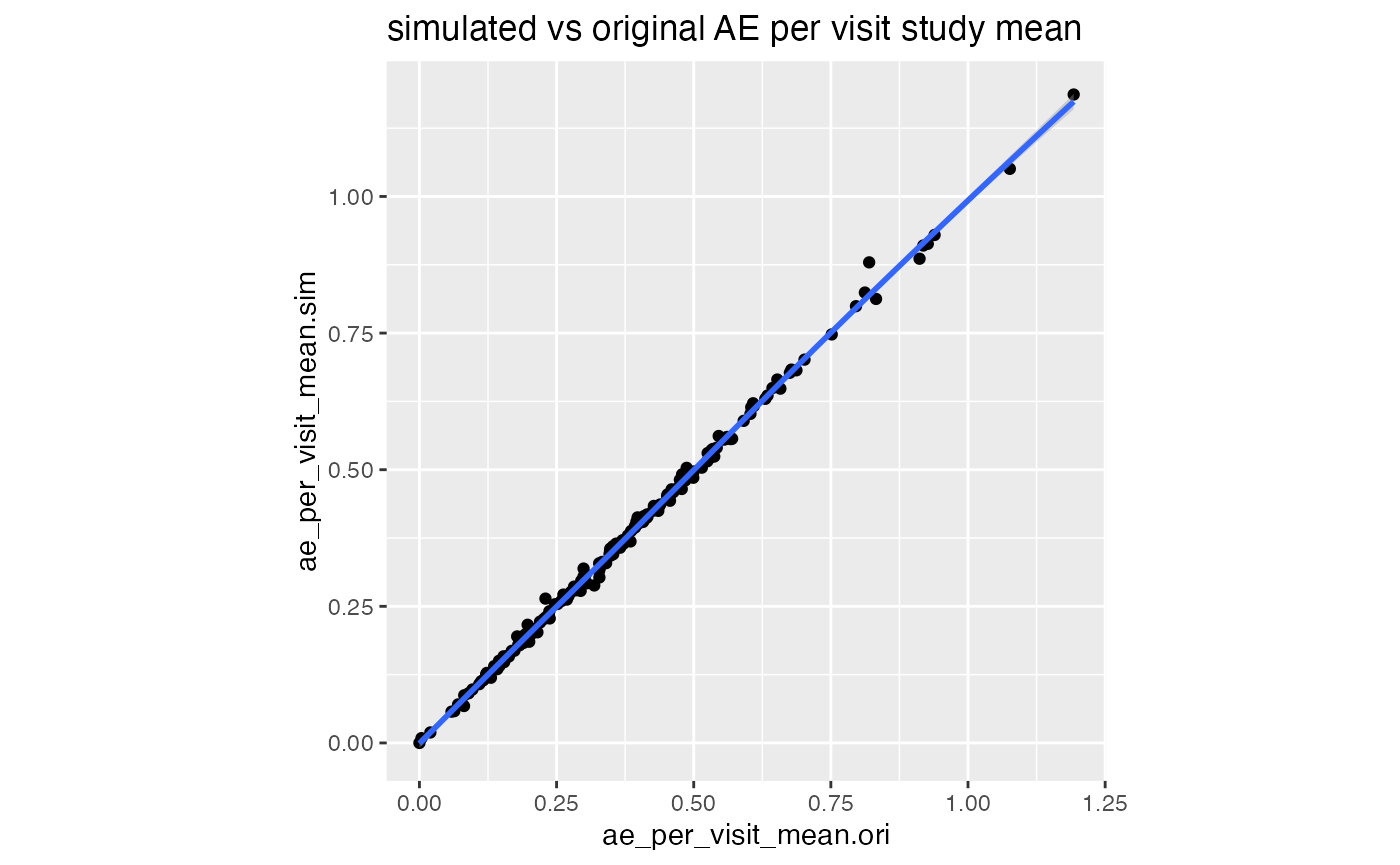

df_comp %>%
  ggplot(aes(max_visit_sd.ori, max_visit_sd.sim)) +
    geom_point() +
    geom_smooth() +
    geom_abline(slope = 1, color = "red") +
    labs(title = "simulated vs original max visit sd site") +
    theme(aspect.ratio = 1)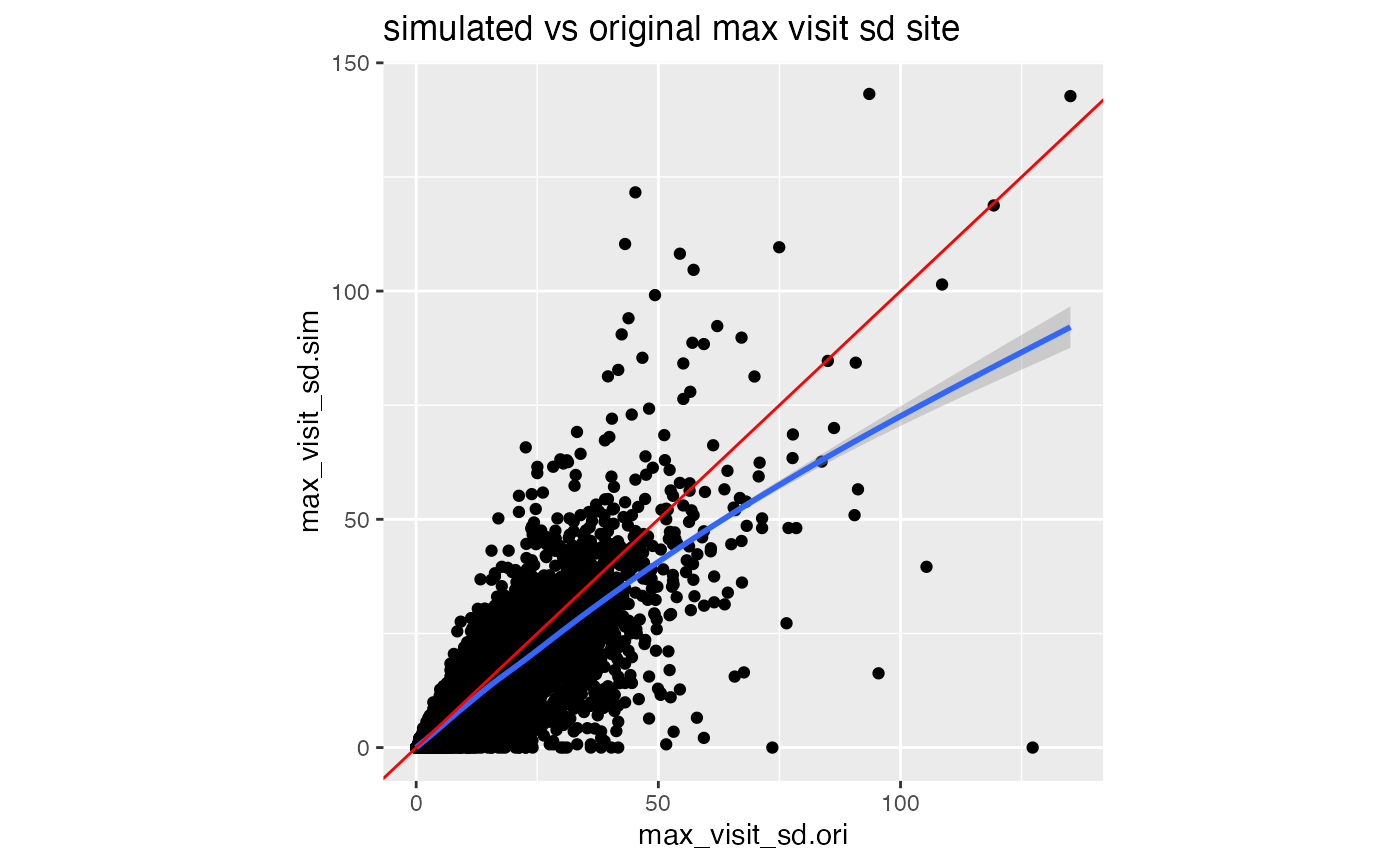

In our portfolio simulation we sample the patient maximum visit values from a normal distribution. If that returns values smaller than 1 we replace it with one. The larger the SD values compared to the mean values the more likely we will sample a patient maximum visit smaller than one. Every time we have to do that correction we are lowering the patient maximum visit SD in our simulation, which we can see in the graph above.

df_comp %>%
  ggplot(aes(max_visit_mean.ori, max_visit_mean.sim)) +
    geom_point() +
    geom_smooth() +
    geom_abline(slope = 1, color = "red") +
    labs(title = "simulated vs original max visit mean site") +
    theme(aspect.ratio = 1)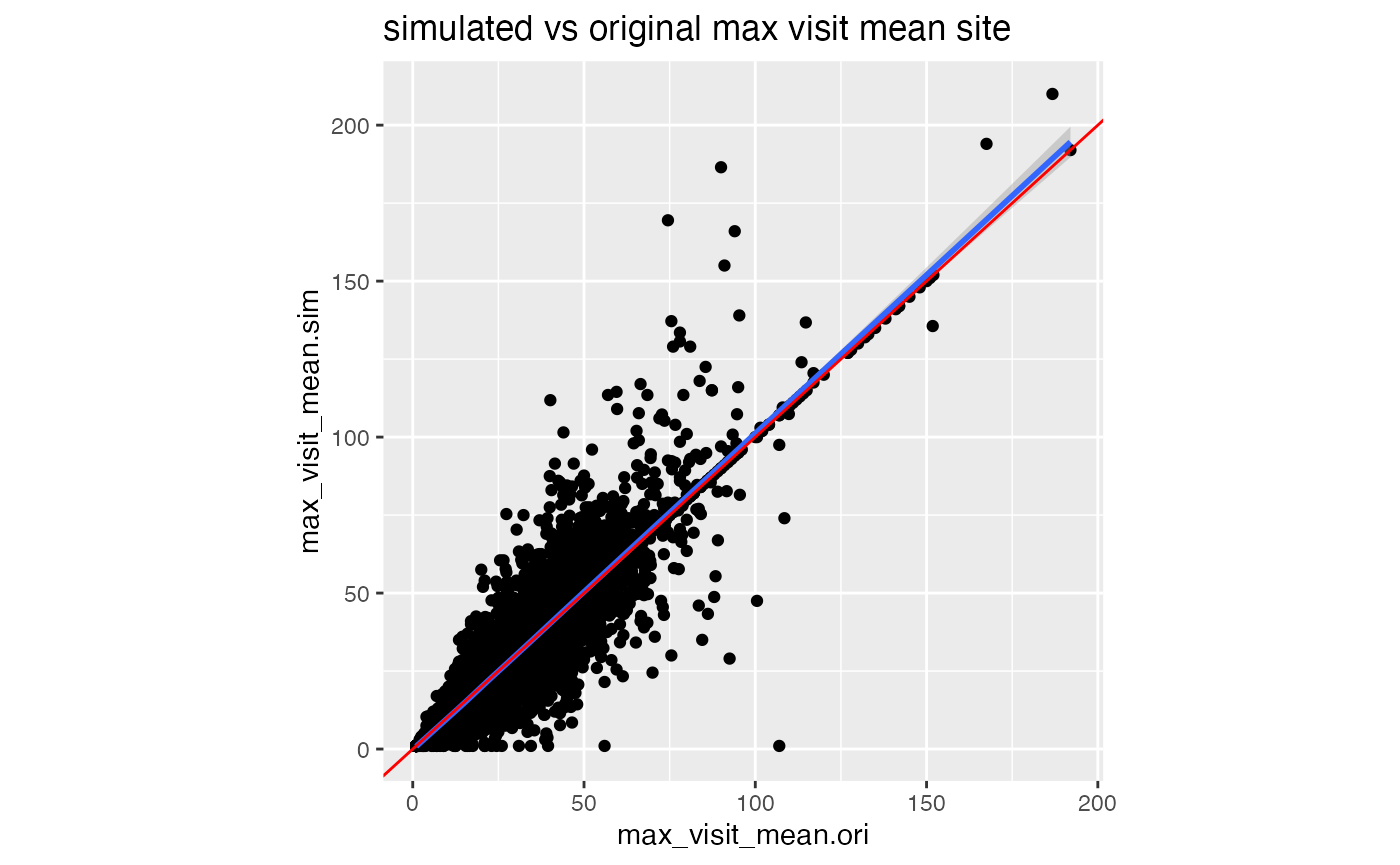

df_comp %>%
  ggplot(aes(n_pat.ori, n_pat.sim)) +
    geom_point() +
    geom_smooth() +
    labs(title = "simulated vs original n_pat site") +
    theme(aspect.ratio = 1)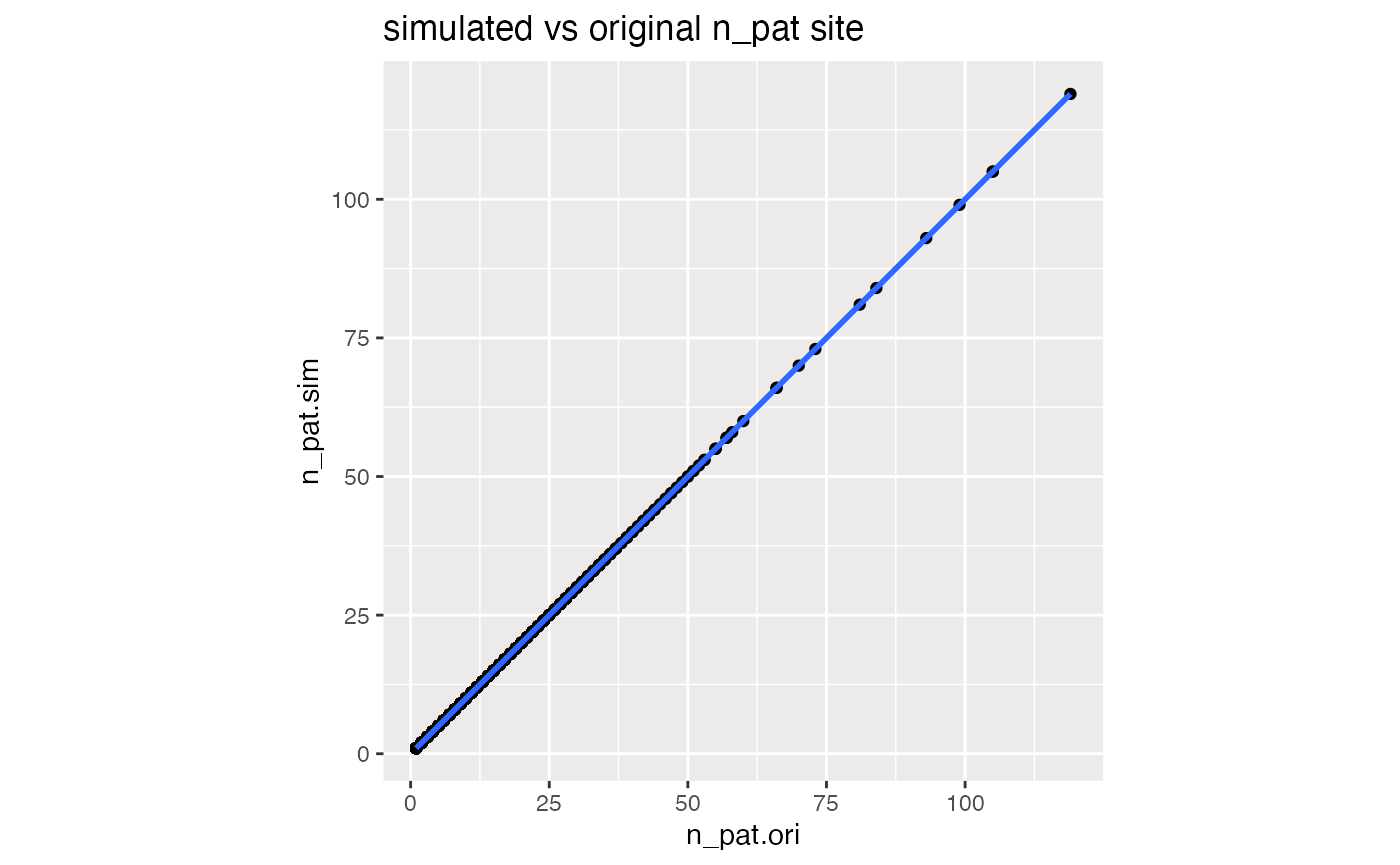

Get Under-Reporting Probability for Different Under Reporting Scenarios

The performance of detecting AE under-reporting is dependent on three things:

the higher the mean AE per visit on study level the better
the higher the number of patients at an under-reporting site the better
the higher the maximum visit number per patient the better
the higher the number of under-reporting sites in a study the worse

In our initial usability assessment we have fixed those parameters. Here we are going leave them as they are in the portfolio. The vanilla version of our artificial portfolio data does not contain any under-reporting sites yet. However simaerep::sim_ur_scenarios() will apply under-reporting scenarios to each site. Reducing the number of AEs by a given under-reporting rate (ur_rate) for all patients at the site and add the corresponding under-reporting statistics.

df_scen <- sim_ur_scenarios(
   df_portf,
   extra_ur_sites = 0,
   ur_rate = c(0.1, 0.25, 0.5, 0.75, 1),
   parallel = TRUE,
   poisson = TRUE,
   prob_lower = TRUE,
   progress = TRUE
)


readr::write_csv(df_scen, file = "scen.csv")

df_scen <- readr::read_csv("scen.csv")


df_scen %>%
  head(25) %>%
  knitr::kable()

study_id	site_number	frac_pat_with_ur	ur_rate	n_pat	n_pat_with_med75	visit_med75	mean_ae_site_med75	mean_ae_study_med75	n_pat_with_med75_study	pval	prob_low	pval_adj	pval_prob_ur	prob_low_adj	prob_low_prob_ur
0001	0001	0.0000000	0.00	2	2	22	3.500000	5.794520	73	0.2289104	0.119	1.0000000	0.0000000	0.8045714	0.1954286
0001	0001	0.0266667	0.10	2	2	22	3.150000	5.794520	73	1.0000000	0.052	1.0000000	0.0000000	0.7392000	0.2608000
0001	0001	0.0266667	0.25	2	2	22	2.625000	5.794520	73	1.0000000	0.020	1.0000000	0.0000000	0.4400000	0.5600000
0001	0001	0.0266667	0.50	2	2	22	1.750000	5.794520	73	1.0000000	0.006	1.0000000	0.0000000	0.2640000	0.7360000
0001	0001	0.0266667	0.75	2	2	22	0.875000	5.794520	73	1.0000000	0.002	1.0000000	0.0000000	0.0880000	0.9120000
0001	0001	0.0266667	1.00	2	2	22	0.000000	5.794520	73	0.0000248	0.000	0.0010908	0.9989092	0.0000000	1.0000000
0001	0002	0.0000000	0.00	2	2	25	9.000000	6.454546	55	1.0000000	1.000	1.0000000	0.0000000	1.0000000	0.0000000
0001	0002	0.0350877	0.10	2	2	25	8.100000	6.454546	55	1.0000000	1.000	1.0000000	0.0000000	1.0000000	0.0000000
0001	0002	0.0350877	0.25	2	2	25	6.750000	6.454546	55	1.0000000	1.000	1.0000000	0.0000000	1.0000000	0.0000000
0001	0002	0.0350877	0.50	2	2	25	4.500000	6.454546	55	0.3898165	0.192	1.0000000	0.0000000	0.8080000	0.1920000
0001	0002	0.0350877	0.75	2	2	25	2.250000	6.454546	55	1.0000000	0.006	1.0000000	0.0000000	0.2640000	0.7360000
0001	0002	0.0350877	1.00	2	2	25	0.000000	6.454546	55	0.0000073	0.002	0.0003225	0.9996775	0.0880000	0.9120000
0001	0003	0.0000000	0.00	4	4	18	4.000000	4.843137	102	0.5600287	0.277	1.0000000	0.0000000	1.0000000	0.0000000
0001	0003	0.0377358	0.10	4	4	18	3.600000	4.843137	102	1.0000000	0.133	1.0000000	0.0000000	0.7315000	0.2685000
0001	0003	0.0377358	0.25	4	4	18	3.000000	4.843137	102	0.1023889	0.049	1.0000000	0.0000000	0.7040000	0.2960000
0001	0003	0.0377358	0.50	4	4	18	2.000000	4.843137	102	0.0067275	0.007	0.2960087	0.7039913	0.3080000	0.6920000
0001	0003	0.0377358	0.75	4	4	18	1.000000	4.843137	102	0.0000794	0.000	0.0034928	0.9965072	0.0000000	1.0000000
0001	0003	0.0377358	1.00	4	4	18	0.000000	4.843137	102	0.0000000	0.000	0.0000004	0.9999996	0.0000000	1.0000000
0001	0004	0.0000000	0.00	6	6	22	4.666667	5.826087	69	0.2860984	0.169	1.0000000	0.0000000	0.8262222	0.1737778
0001	0004	0.0800000	0.10	6	6	22	4.200000	5.826087	69	1.0000000	0.054	1.0000000	0.0000000	0.7040000	0.2960000
0001	0004	0.0800000	0.25	6	6	22	3.500000	5.826087	69	0.0194500	0.007	0.4913096	0.5086904	0.3080000	0.6920000
0001	0004	0.0800000	0.50	6	6	22	2.333333	5.826087	69	0.0001854	0.000	0.0081566	0.9918434	0.0000000	1.0000000
0001	0004	0.0800000	0.75	6	6	22	1.166667	5.826087	69	0.0000000	0.000	0.0000020	0.9999980	0.0000000	1.0000000
0001	0004	0.0800000	1.00	6	6	22	0.000000	5.826087	69	0.0000000	0.000	0.0000000	1.0000000	0.0000000	1.0000000
0001	0005	0.0000000	0.00	1	1	30	7.000000	8.035714	28	0.8579445	0.527	1.0000000	0.0000000	1.0000000	0.0000000

Portfolio Performance

For every site in the portfolio we have now generated the AE under-reporting probability for the following under-reporting rates 0, 0.25, 0.5, 0.75 and 1:

df_scen %>%
  select(study_id, site_number, ur_rate, prob_low_prob_ur) %>%
  head(25) %>%
  knitr::kable()

study_id	site_number	ur_rate	prob_low_prob_ur
0001	0001	0.00	0.1954286
0001	0001	0.10	0.2608000
0001	0001	0.25	0.5600000
0001	0001	0.50	0.7360000
0001	0001	0.75	0.9120000
0001	0001	1.00	1.0000000
0001	0002	0.00	0.0000000
0001	0002	0.10	0.0000000
0001	0002	0.25	0.0000000
0001	0002	0.50	0.1920000
0001	0002	0.75	0.7360000
0001	0002	1.00	0.9120000
0001	0003	0.00	0.0000000
0001	0003	0.10	0.2685000
0001	0003	0.25	0.2960000
0001	0003	0.50	0.6920000
0001	0003	0.75	1.0000000
0001	0003	1.00	1.0000000
0001	0004	0.00	0.1737778
0001	0004	0.10	0.2960000
0001	0004	0.25	0.6920000
0001	0004	0.50	1.0000000
0001	0004	0.75	1.0000000
0001	0004	1.00	1.0000000
0001	0005	0.00	0.0000000

We usually recommend a 0.95 threshold to flag sites as under-reporting. We can use this threshold to calculate the ratio of flagged sites per under-reporting rate. The zero under-reporting scenario defines the expected false positive rates (fpr as fp/N), while the other scenarios give us the expected true positive rate (tpr as tp/P) for sites with that under-reporting level. The condition for the tpr and fpr rates for the simulated portfolio is that each site is the only under-reporting site in the respective study.

df_perf_portf <- df_scen %>%
  mutate(is_ur = prob_low_prob_ur >= 0.95) %>%
  group_by(ur_rate, is_ur) %>%
  count() %>%
  pivot_wider(
    names_from = is_ur,
    values_from = n,
    names_prefix = "is_ur_"
  ) %>%
  mutate(
    n_sites = is_ur_TRUE + is_ur_FALSE,
    ratio = is_ur_TRUE / n_sites,
    ratio_type = ifelse(ur_rate == 0, "fpr", "tpr"),
    ci95_low = prop.test(is_ur_TRUE, n_sites)$conf.int[1],
    ci95_high = prop.test(is_ur_TRUE, n_sites)$conf.int[2]
  ) 

df_perf_portf %>%
  knitr::kable(digits = 3)

ur_rate	is_ur_FALSE	is_ur_TRUE	n_sites	ratio	ratio_type	ci95_low	ci95_high
0.00	15662	12	15674	0.001	fpr	0.000	0.001
0.10	15601	73	15674	0.005	tpr	0.004	0.006
0.25	14874	800	15674	0.051	tpr	0.048	0.055
0.50	11496	4178	15674	0.267	tpr	0.260	0.274
0.75	8172	7502	15674	0.479	tpr	0.471	0.486
1.00	6467	9207	15674	0.587	tpr	0.580	0.595

Benchmark {simaerep} Using Portfolio Performance

Performance Under Optimal Conditions

True positive rates for sites with with an under-reporting rate of 1 is surprisingly small. We would expect that here we should have true positive ratios of close to 100%. The reason is that within a portfolio we have sites that are just starting up and have not reported any AEs yet. We also have studies with overall low AE rates for example for studies with healthy participants. Altogether this allows uncompliant sites to hide among the compliant sites which makes it more difficult to detect them. Therefore we would also like to demonstrate {simaerep} performance as it can be expected under ideal conditions.

We generate studies with the following parameters:

200 patients
20 sites
one under-reporting site
0.5 AEs per visit
in average 20 visits per patient with SD of 2

We simulate 500 studies for each under-reporting scenario.

standard_sim <- function(ur_rate, seed) {
  set.seed(seed)
  df <- sim_test_data_study(
    n_pat = 200,
    n_sites = 20,
    frac_site_with_ur = 0.05,
    ur_rate = ur_rate,
    ae_per_visit_mean = 0.5,
    max_visit_mean = 20,
    max_visit_sd = 2
  )
  
  if(ur_rate == 0) {
    df$is_ur <- FALSE
  }
  
  return(df)
}

df_data_grid <- tibble(
    ur_rate = c(0, 0.1, 0.25, 0.5, 0.75, 1),
    seed = list(seq(1, 500))
  ) %>%
 unnest(seed) %>%
 mutate(
   data = map2(ur_rate, seed, standard_sim)
 ) 

df_data_grid

## # A tibble: 3,000 × 3
##    ur_rate  seed data                
##      <dbl> <int> <list>              
##  1       0     1 <tibble [3,891 × 8]>
##  2       0     2 <tibble [3,892 × 8]>
##  3       0     3 <tibble [3,891 × 8]>
##  4       0     4 <tibble [3,866 × 8]>
##  5       0     5 <tibble [3,899 × 8]>
##  6       0     6 <tibble [3,887 × 8]>
##  7       0     7 <tibble [3,927 × 8]>
##  8       0     8 <tibble [3,869 × 8]>
##  9       0     9 <tibble [3,884 × 8]>
## 10       0    10 <tibble [3,884 × 8]>
## # ℹ 2,990 more rows

df_visit <- df_data_grid %>%
  mutate(
    study_id = paste0(
      "study-", 
      str_pad(ur_rate, width= 3, side = "left", pad = "0"),
      "-",
      seed
      )
  ) %>%
  unnest(data)

df_visit %>%
  head(25) %>%
  knitr::kable()

seed	patnum	site_number	is_ur	max_visit_mean	max_visit_sd	ae_per_visit_mean	visit	n_ae	study_id
1	P000001	S0001	FALSE	20	2	0.5	1	0	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	2	1	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	3	1	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	4	2	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	5	4	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	6	5	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	7	6	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	8	6	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	9	6	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	10	6	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	11	7	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	12	7	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	13	8	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	14	8	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	15	9	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	16	12	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	17	12	study-000-1
1	P000001	S0001	FALSE	20	2	0.5	18	13	study-000-1
1	P000002	S0001	FALSE	20	2	0.5	1	1	study-000-1
1	P000002	S0001	FALSE	20	2	0.5	2	1	study-000-1
1	P000002	S0001	FALSE	20	2	0.5	3	1	study-000-1
1	P000002	S0001	FALSE	20	2	0.5	4	1	study-000-1
1	P000002	S0001	FALSE	20	2	0.5	5	1	study-000-1
1	P000002	S0001	FALSE	20	2	0.5	6	1	study-000-1
1	P000002	S0001	FALSE	20	2	0.5	7	2	study-000-1

Next we apply {simaerep}

df_site <- site_aggr(df_visit)

df_sim_sites <- sim_sites(df_site, df_visit)

df_eval <- eval_sites(df_sim_sites)

We calculate the confusion matrices.

df_perf <- df_visit %>%
  select(ur_rate, study_id, site_number, is_ur) %>%
  distinct() %>%
  left_join(df_eval, by = c("study_id", "site_number")) %>%
  mutate(is_ur_detected = prob_low_prob_ur >= 0.95) %>%
  group_by(ur_rate, is_ur, is_ur_detected) %>%
  count()

readr::write_csv(df_perf, file = "scen_st.csv")
remove(df_visit) # free up RAM

df_perf <- readr::read_csv(file = "scen_st.csv")

df_perf %>%
  knitr::kable()

ur_rate	is_ur	is_ur_detected	n
0.00	FALSE	FALSE	9977
0.00	FALSE	TRUE	23
0.10	FALSE	FALSE	9482
0.10	FALSE	TRUE	18
0.10	TRUE	FALSE	486
0.10	TRUE	TRUE	14
0.25	FALSE	FALSE	9486
0.25	FALSE	TRUE	14
0.25	TRUE	FALSE	364
0.25	TRUE	TRUE	136
0.50	FALSE	FALSE	9487
0.50	FALSE	TRUE	13
0.50	TRUE	FALSE	12
0.50	TRUE	TRUE	488
0.75	FALSE	FALSE	9499
0.75	FALSE	TRUE	1
0.75	TRUE	TRUE	500
1.00	FALSE	FALSE	9500
1.00	TRUE	TRUE	500

We calculate tpr and fpr.

get_prop_test_ci95 <- function(..., ix) {
  
  stopifnot(ix %in% c(1, 2))
  
  tryCatch(
    prop.test(...)$conf.int[ix],
    error = function(cnd) c(NA, NA)[ix]
  )
}

df_perf_st <- df_perf %>%
  group_by(ur_rate) %>%
  summarize(
    N = sum(ifelse(! is_ur, n, 0)),
    P = sum(ifelse(is_ur, n, 0)),
    TP = sum(ifelse(is_ur & is_ur_detected, n, 0)),
    FP = sum(ifelse(! is_ur & is_ur_detected, n, 0)),
    TN = sum(ifelse(! is_ur & ! is_ur_detected, n, 0)),
    FN = sum(ifelse(is_ur & ! is_ur_detected, n, 0))
  ) %>%
  mutate(
    tpr = TP / P,
    tpr_ci95_low = map2_dbl(TP, P, get_prop_test_ci95, ix = 1),
    tpr_ci95_high = map2_dbl(TP, P, get_prop_test_ci95, ix = 2),
    fpr = FP / N,
    fpr_ci95_low = map2_dbl(FP, N, get_prop_test_ci95, ix = 1),
    fpr_ci95_high = map2_dbl(FP, N, get_prop_test_ci95, ix = 2)
  )

df_perf_st %>%
  knitr::kable(digit = 4)

ur_rate	N	P	TP	FP	TN	FN	tpr	tpr_ci95_low	tpr_ci95_high	fpr	fpr_ci95_low	fpr_ci95_high
0.00	10000	0	0	23	9977	0	NaN	NA	NA	0.0023	0.0015	0.0035
0.10	9500	500	14	18	9482	486	0.028	0.0160	0.0477	0.0019	0.0012	0.0031
0.25	9500	500	136	14	9486	364	0.272	0.2339	0.3137	0.0015	0.0008	0.0025
0.50	9500	500	488	13	9487	12	0.976	0.9573	0.9869	0.0014	0.0008	0.0024
0.75	9500	500	500	1	9499	0	1.000	0.9905	1.0000	0.0001	0.0000	0.0007
1.00	9500	500	500	0	9500	0	1.000	0.9905	1.0000	0.0000	0.0000	0.0005

Under ideal conditions sites with 0.5 under-reporting rate or more will almost all get flagged with a ratio of 0.97 or more with minimal ratio for false positive flags < 0.003.

Effect of Adjusting visit_med75

One of the latest update to simaerep was an improvement to the visit_med75 calculation. We can check how this has affected portfolio performance. We find that we have most likely slightly increased performance.

df_scen_old_visit_med75 <- sim_ur_scenarios(
   df_portf,
   extra_ur_sites = 5,
   ur_rate = c(0.1, 0.25, 0.5, 0.75, 1),
   parallel = TRUE,
   poisson = TRUE,
   prob_lower = TRUE,
   progress = TRUE,
   site_aggr_args = list(method = "med75") # default is "med75_adj"
) 

readr::write_csv(df_scen_old_visit_med75, file = "scen_old.csv")

df_scen_old_visit_med75 <- readr::read_csv("scen_old.csv")

df_scen_old_visit_med75 %>%
  head(25) %>%
  knitr::kable()

study_id	site_number	extra_ur_sites	frac_pat_with_ur	ur_rate	n_pat	n_pat_with_med75	visit_med75	mean_ae_site_med75	mean_ae_study_med75	n_pat_with_med75_study	pval	prob_low	pval_adj	pval_prob_ur	prob_low_adj	prob_low_prob_ur
0001	0001	0	0.0000000	0.00	2	2	17	2.0	4.570093	107	0.0933704	0.032	1.0000000	0.0000000	0.3520000	0.6480000
0001	0001	0	0.0183486	0.10	2	2	17	1.8	4.570093	107	1.0000000	0.013	1.0000000	0.0000000	0.1906667	0.8093333
0001	0001	0	0.0183486	0.25	2	2	17	1.5	4.570093	107	0.0415023	0.013	0.6087005	0.3912995	0.1906667	0.8093333
0001	0001	0	0.0183486	0.50	2	2	17	1.0	4.570093	107	0.0108238	0.003	0.2966466	0.7033534	0.0880000	0.9120000
0001	0001	0	0.0183486	0.75	2	2	17	0.5	4.570093	107	0.0020871	0.000	0.0918333	0.9081667	0.0000000	1.0000000
0001	0001	0	0.0183486	1.00	2	2	17	0.0	4.570093	107	0.0002580	0.000	0.0113519	0.9886481	0.0000000	1.0000000
0001	0001	1	0.0410759	0.10	2	2	17	1.8	4.561682	107	1.0000000	0.013	1.0000000	0.0000000	0.1906667	0.8093333
0001	0001	1	0.0410759	0.25	2	2	17	1.5	4.549065	107	1.0000000	0.013	1.0000000	0.0000000	0.1906667	0.8093333
0001	0001	1	0.0410759	0.50	2	2	17	1.0	4.528037	107	1.0000000	0.003	1.0000000	0.0000000	0.0880000	0.9120000
0001	0001	1	0.0410759	0.75	2	2	17	0.5	4.507009	107	1.0000000	0.000	1.0000000	0.0000000	0.0000000	1.0000000
0001	0001	1	0.0410759	1.00	2	2	17	0.0	4.485981	107	0.0002466	0.001	0.0108502	0.9891498	0.0440000	0.9560000
0001	0001	2	0.0638032	0.10	2	2	17	1.8	4.550467	107	1.0000000	0.014	1.0000000	0.0000000	0.2053333	0.7946667
0001	0001	2	0.0638032	0.25	2	2	17	1.5	4.521028	107	1.0000000	0.014	1.0000000	0.0000000	0.2053333	0.7946667
0001	0001	2	0.0638032	0.50	2	2	17	1.0	4.471963	107	1.0000000	0.004	1.0000000	0.0000000	0.0880000	0.9120000
0001	0001	2	0.0638032	0.75	2	2	17	0.5	4.422897	107	1.0000000	0.001	1.0000000	0.0000000	0.0440000	0.9560000
0001	0001	2	0.0638032	1.00	2	2	17	0.0	4.373832	107	0.0003766	0.005	0.0165706	0.9834294	0.1100000	0.8900000
0001	0001	3	0.0865304	0.10	2	2	17	1.8	4.543925	107	1.0000000	0.014	1.0000000	0.0000000	0.2053333	0.7946667
0001	0001	3	0.0865304	0.25	2	2	17	1.5	4.504673	107	0.0410564	0.014	0.6021598	0.3978402	0.2053333	0.7946667
0001	0001	3	0.0865304	0.50	2	2	17	1.0	4.439252	107	0.0152860	0.004	0.2966466	0.7033534	0.0880000	0.9120000
0001	0001	3	0.0865304	0.75	2	2	17	0.5	4.373832	107	0.0029791	0.001	0.1310801	0.8689199	0.0440000	0.9560000
0001	0001	3	0.0865304	1.00	2	2	17	0.0	4.308411	107	0.0003629	0.007	0.0159689	0.9840311	0.1540000	0.8460000
0001	0001	4	0.1092577	0.10	2	2	17	1.8	4.533645	107	1.0000000	0.014	1.0000000	0.0000000	0.2053333	0.7946667
0001	0001	4	0.1092577	0.25	2	2	17	1.5	4.478972	107	1.0000000	0.014	1.0000000	0.0000000	0.2053333	0.7946667
0001	0001	4	0.1092577	0.50	2	2	17	1.0	4.387850	107	1.0000000	0.004	1.0000000	0.0000000	0.0880000	0.9120000
0001	0001	4	0.1092577	0.75	2	2	17	0.5	4.296729	107	1.0000000	0.001	1.0000000	0.0000000	0.0440000	0.9560000

df_perf_portf_old_visit_med75 <- df_scen_old_visit_med75 %>%
  mutate(is_ur = prob_low_prob_ur >= 0.95) %>%
  group_by(ur_rate, is_ur) %>%
  count() %>%
  pivot_wider(
    names_from = is_ur,
    values_from = n,
    names_prefix = "is_ur_"
  ) %>%
  mutate(
    n_sites = is_ur_TRUE + is_ur_FALSE,
    ratio = is_ur_TRUE / n_sites,
    ratio_type = ifelse(ur_rate == 0, "fpr", "tpr"),
    ci95_low = prop.test(is_ur_TRUE, n_sites)$conf.int[1],
    ci95_high = prop.test(is_ur_TRUE, n_sites)$conf.int[2]
  ) 

df_perf_portf_old_visit_med75 %>%
  knitr::kable(digits = 3)

ur_rate	is_ur_FALSE	is_ur_TRUE	is_ur_NA	n_sites	ratio	ratio_type	ci95_low	ci95_high
0.00	15662	8	4	15670	0.001	fpr	0.000	0.001
0.10	93680	340	24	94020	0.004	tpr	0.003	0.004
0.25	90404	3616	24	94020	0.038	tpr	0.037	0.040
0.50	74704	19316	24	94020	0.205	tpr	0.203	0.208
0.75	57340	36680	24	94020	0.390	tpr	0.387	0.393
1.00	49050	44970	24	94020	0.478	tpr	0.475	0.482

Days vs. Visits

Instead of normalising the AEs per patient by visit an alternative could be to normalise by the number of days that have passed since the patients enrollment. {simaerep} can be used for both types of normalisation which is demonstrated here. But normalising by days is a bit more complex as it creates more data points.

The maximum number of days per patient can be up to several years, so > 1000 days. simaerep exposes implicitly missing entries which can lead to single patients having 1000 entries or more, one entry for each day on the study. In order to avoid to generate a huge portfolio data frame we preserve memory by wrapping sim_test_data_portfolio() and sim_ur_scenarios() into a single call and apply it per study.

wr <- function(df) {
  df_portf <- sim_test_data_portfolio(df, parallel = FALSE, progress = FALSE)
  df_scen <- sim_ur_scenarios(df_portf,
                               extra_ur_sites = 5,
                               ur_rate = c(0.1, 0.25, 0.5, 0.75, 1),
                               parallel = FALSE,
                               poisson = TRUE,
                               prob_lower = TRUE,
                               progress = FALSE)
  return(df_scen)
}

df_prep <- df_config %>%
  select(- max_visit_sd, - max_visit_mean, - ae_per_visit_mean) %>%
  rename(max_visit_sd = max_days_sd,
         max_visit_mean = max_days_mean,
         ae_per_visit_mean = ae_per_day_mean) %>%
  group_by(study_id_gr = study_id) %>%
  nest() %>%
  ungroup() 

progressr::with_progress(
  df_scen_days <- df_prep %>%
    mutate(data = purrr_bar(
      .data$data,
      .purrr = furrr::future_map,
      .f = wr,
      .progress = TRUE,
      .steps = nrow(.),
      .purrr_args = list(.options = furrr_options(seed = TRUE))
      )
   )
)

df_scen_days <- df_scen_days %>%
  unnest(data) %>%
  select(- study_id_gr)

readr::write_csv(df_scen_days, file = "scen_days.csv")

df_scen_days <- readr::read_csv("scen_days.csv")

df_scen_days %>%
  head(25) %>%
  knitr::kable()

study_id	site_number	extra_ur_sites	frac_pat_with_ur	ur_rate	n_pat	n_pat_with_med75	visit_med75	mean_ae_site_med75	mean_ae_study_med75	n_pat_with_med75_study	pval	prob_low	pval_adj	pval_prob_ur	prob_low_adj	prob_low_prob_ur
0001	0001	0	0.0000000	0.00	2	2	727	5.00	5.363636	66	1.0000000	0.517	1.0000000	0.0000000	1.0000000	0.0000000
0001	0001	0	0.0294118	0.10	2	2	727	4.50	5.363636	66	0.7553363	0.397	1.0000000	0.0000000	0.9704444	0.0295556
0001	0001	0	0.0294118	0.25	2	2	727	3.75	5.363636	66	1.0000000	0.174	1.0000000	0.0000000	0.7656000	0.2344000
0001	0001	0	0.0294118	0.50	2	2	727	2.50	5.363636	66	0.0853088	0.041	1.0000000	0.0000000	0.3153333	0.6846667
0001	0001	0	0.0294118	0.75	2	2	727	1.25	5.363636	66	1.0000000	0.005	1.0000000	0.0000000	0.1540000	0.8460000
0001	0001	0	0.0294118	1.00	2	2	727	0.00	5.363636	66	0.0000499	0.000	0.0021950	0.9978050	0.0000000	1.0000000
0001	0001	1	0.0571895	0.10	2	2	727	4.50	5.340909	66	1.0000000	0.399	1.0000000	0.0000000	0.9753333	0.0246667
0001	0001	1	0.0571895	0.25	2	2	727	3.75	5.306818	66	1.0000000	0.180	1.0000000	0.0000000	0.7920000	0.2080000
0001	0001	1	0.0571895	0.50	2	2	727	2.50	5.250000	66	1.0000000	0.047	1.0000000	0.0000000	0.3446667	0.6553333
0001	0001	1	0.0571895	0.75	2	2	727	1.25	5.193182	66	1.0000000	0.008	1.0000000	0.0000000	0.1760000	0.8240000
0001	0001	1	0.0571895	1.00	2	2	727	0.00	5.136364	66	0.0000723	0.003	0.0031792	0.9968208	0.1320000	0.8680000
0001	0001	2	0.0849673	0.10	2	2	727	4.50	5.319697	66	1.0000000	0.399	1.0000000	0.0000000	0.9753333	0.0246667
0001	0001	2	0.0849673	0.25	2	2	727	3.75	5.253788	66	1.0000000	0.181	1.0000000	0.0000000	0.7964000	0.2036000
0001	0001	2	0.0849673	0.50	2	2	727	2.50	5.143939	66	1.0000000	0.050	1.0000000	0.0000000	0.3666667	0.6333333
0001	0001	2	0.0849673	0.75	2	2	727	1.25	5.034091	66	1.0000000	0.010	1.0000000	0.0000000	0.2200000	0.7800000
0001	0001	2	0.0849673	1.00	2	2	727	0.00	4.924242	66	0.0001056	0.008	0.0046481	0.9953519	0.1760000	0.8240000
0001	0001	3	0.1127451	0.10	2	2	727	4.50	5.309091	66	1.0000000	0.400	1.0000000	0.0000000	0.9777778	0.0222222
0001	0001	3	0.1127451	0.25	2	2	727	3.75	5.227273	66	1.0000000	0.192	1.0000000	0.0000000	0.8280000	0.1720000
0001	0001	3	0.1127451	0.50	2	2	727	2.50	5.090909	66	0.1451010	0.058	1.0000000	0.0000000	0.4235000	0.5765000
0001	0001	3	0.1127451	0.75	2	2	727	1.25	4.954546	66	1.0000000	0.014	1.0000000	0.0000000	0.3080000	0.6920000
0001	0001	3	0.1127451	1.00	2	2	727	0.00	4.818182	66	0.0001619	0.012	0.0071229	0.9928771	0.2640000	0.7360000
0001	0001	4	0.1405229	0.10	2	2	727	4.50	5.293939	66	1.0000000	0.401	1.0000000	0.0000000	0.9802222	0.0197778
0001	0001	4	0.1405229	0.25	2	2	727	3.75	5.189394	66	1.0000000	0.207	1.0000000	0.0000000	0.8280000	0.1720000
0001	0001	4	0.1405229	0.50	2	2	727	2.50	5.015151	66	0.1432160	0.068	1.0000000	0.0000000	0.4235000	0.5765000
0001	0001	4	0.1405229	0.75	2	2	727	1.25	4.840909	66	1.0000000	0.021	1.0000000	0.0000000	0.3153333	0.6846667

df_perf_portf_days <- df_scen_days %>%
  mutate(is_ur = prob_low_prob_ur >= 0.95) %>%
  group_by(ur_rate, is_ur) %>%
  count() %>%
  pivot_wider(
    names_from = is_ur,
    values_from = n,
    names_prefix = "is_ur_"
  ) %>%
  mutate(
    n_sites = is_ur_TRUE + is_ur_FALSE,
    ratio = is_ur_TRUE / n_sites,
    ratio_type = ifelse(ur_rate == 0, "fpr", "tpr"),
    ci95_low = prop.test(is_ur_TRUE, n_sites)$conf.int[1],
    ci95_high = prop.test(is_ur_TRUE, n_sites)$conf.int[2]
  ) 

df_perf_portf_days %>%
  knitr::kable(digits = 3)

ur_rate	is_ur_FALSE	is_ur_TRUE	n_sites	ratio	ratio_type	ci95_low	ci95_high
0.00	14441	7	14448	0.000	fpr	0.000	0.001
0.10	86141	547	86688	0.006	tpr	0.006	0.007
0.25	80821	5867	86688	0.068	tpr	0.066	0.069
0.50	66036	20652	86688	0.238	tpr	0.235	0.241
0.75	54199	32489	86688	0.375	tpr	0.372	0.378
1.00	51520	35168	86688	0.406	tpr	0.402	0.409

Heuristic Rank

Instead of using {simaerep} we can also use a heuristic method based on AE per visit and apply that to the simulated portfolio with different scenarios of under-reporting

Flag 5% (always round up) of all sites in a study that have the lowest AE per visit rate.
Always flag sites with no AEs.

df_ae_per_vs <-df_portf %>%
  group_by(study_id, site_number, patnum) %>%
  filter(visit == max(visit)) %>%
  group_by(study_id, site_number) %>%
  summarise(visit = sum(visit),
            n_ae = sum(n_ae),
            .groups = "drop") %>%
  mutate(ae_per_visit = n_ae / visit) %>%
  group_by(study_id) %>%
  mutate(
    ls_study_ae_per_visit = list(ae_per_visit),
    rwn = row_number(),
    # we take out site ae_per_visit from study pool
    ls_study_ae_per_visit = map2(
        ls_study_ae_per_visit, rwn,
        function(ls, rwn) ls[- rwn]
      )
  ) %>%
  select(- rwn) %>%
  ungroup()

df_ae_per_vs

## # A tibble: 15,674 × 6
##    study_id site_number visit  n_ae ae_per_visit ls_study_ae_per_visit
##    <chr>    <chr>       <int> <int>        <dbl> <list>               
##  1 0001     0001           44    13        0.295 <dbl [43]>           
##  2 0001     0002           53    15        0.283 <dbl [43]>           
##  3 0001     0003           74    19        0.257 <dbl [43]>           
##  4 0001     0004          215    57        0.265 <dbl [43]>           
##  5 0001     0005           30     9        0.3   <dbl [43]>           
##  6 0001     0006           35    11        0.314 <dbl [43]>           
##  7 0001     0007           36    14        0.389 <dbl [43]>           
##  8 0001     0008          172    37        0.215 <dbl [43]>           
##  9 0001     0009           40    19        0.475 <dbl [43]>           
## 10 0001     0010          137    32        0.234 <dbl [43]>           
## # ℹ 15,664 more rows

We write a function that: - determines how many sites should be flagged in a study - pools ae_per_visit rates and ranks sites (using dense_rank()) - site gets flagged if the specific rank for a site is within the number of sites that should get flagged

flag_heuristics_rnk <- function(ae_per_visit, ls_study_ae_per_visit) {
  
  n_flags <- ceiling(length(ls_study_ae_per_visit + 1) * 0.05)

  rnk <- tibble(ae_per_visit = ae_per_visit, site = "site") %>%
    bind_rows(
      tibble(ae_per_visit = ls_study_ae_per_visit, site = "other")
    ) %>%
    # using dense_rank will assign rank 1 to all sites with lowest rate
    # this is important as there can be many sites with a zero ratio
    # occasionally this will flag more sites than anticipated
    arrange(ae_per_visit, site) %>%
    mutate(rnk = dense_rank(ae_per_visit)) %>%
    filter(site == "site") %>%
    pull(rnk)
  
  return(rnk <= n_flags)
}

flag_heuristics_rnk(
  df_ae_per_vs$ae_per_visit[[1]],
  df_ae_per_vs$ls_study_ae_per_visit[[1]]
)

## [1] FALSE

Next we wrap that function with another function simulates under-reporting

sim_heuristic_ur <- function(ae_per_visit,
                             ls_study_ae_per_visit,
                             ur_rates,
                             .f = flag_heuristics_rnk) {
  tibble(
    ur_rate = ur_rates,
    ae_per_visit = ae_per_visit
  ) %>%
  mutate(
    ae_per_visit = ae_per_visit * (1 - ur_rate),
    is_ur = map_lgl(ae_per_visit, .f, ls_study_ae_per_visit)
  )
}

sim_heuristic_ur(
  df_ae_per_vs$ae_per_visit[[1]],
  df_ae_per_vs$ls_study_ae_per_visit[[1]],
  ur_rates = c(0, 0.1, 0.25, 0.5, 0.75, 1)
)

## # A tibble: 6 × 3
##   ur_rate ae_per_visit is_ur
##     <dbl>        <dbl> <lgl>
## 1    0          0.295  FALSE
## 2    0.1        0.266  FALSE
## 3    0.25       0.222  FALSE
## 4    0.5        0.148  TRUE 
## 5    0.75       0.0739 TRUE 
## 6    1          0      TRUE

We apply.

progressr::with_progress(
  df_perf_heuristic_rnk <- df_ae_per_vs %>%
    mutate(
      sim = simaerep::purrr_bar(
        ae_per_visit, ls_study_ae_per_visit,
        .purrr = furrr::future_map2,
        .f = sim_heuristic_ur,
        .f_args = list(ur_rates = c(0, 0.1, 0.25, 0.5, 0.75, 1)),
        .steps = nrow(.)
      )
    )
)

df_perf_heuristic_rnk <- df_perf_heuristic_rnk %>%
  select(sim) %>%
  unnest(sim) %>%
  group_by(ur_rate) %>%
  summarise(
    is_ur = sum(is_ur),
    n_sites = n(),
    .groups = "drop"
  ) %>%
  mutate(
    ratio = is_ur / n_sites,
    ratio_type = ifelse(ur_rate == 0, "fpr", "tpr"),
    ci95_low = map2_dbl(is_ur, n_sites, get_prop_test_ci95, ix = 1),
    ci95_high = map2_dbl(is_ur, n_sites, get_prop_test_ci95, ix = 2),
  )

readr::write_csv(df_perf_heuristic_rnk, file = "heuristic_rnk.csv")

We see that this method is generously flagging sites resulting in good tpr at the cost of a high fpr. By default at least one site per study gets flagged.

df_perf_heuristic_rnk <- readr::read_csv(file = "heuristic_rnk.csv")

df_perf_heuristic_rnk %>%
  knitr::kable(digits = 3)

ur_rate	is_ur	n_sites	ratio	ratio_type	ci95_low	ci95_high
0.00	1560	15674	0.100	fpr	0.095	0.104
0.10	2134	15674	0.136	tpr	0.131	0.142
0.25	4716	15674	0.301	tpr	0.294	0.308
0.50	11753	15674	0.750	tpr	0.743	0.757
0.75	15197	15674	0.970	tpr	0.967	0.972
1.00	15674	15674	1.000	tpr	1.000	1.000

Heuristic Box Plot Outlier

We can also imagine a heuristic that tries to detect lower boundary outliers on the basis of the ae per visit rate. This should be flagging more conservatively without flagging sites by default. A simple non-parametric method for outlier detection is to calculate box plot statistic and to flag all points that are below the lower whisker boundary.

flag_heuristics_box <- function(ae_per_visit, ls_study_ae_per_visit) {
  
  min_whisker <- min(boxplot.stats(c(ae_per_visit, ls_study_ae_per_visit))$stats)
  return(ae_per_visit < min_whisker)
  
}

flag_heuristics_box(
  df_ae_per_vs$ae_per_visit[[1]],
  df_ae_per_vs$ls_study_ae_per_visit[[1]]
)

## [1] FALSE

flag_heuristics_box(
  0,
  df_ae_per_vs$ls_study_ae_per_visit[[1]]
)

## [1] TRUE

We apply.

progressr::with_progress(
  df_perf_heuristic_box <- df_ae_per_vs %>%
    mutate(
      sim = simaerep::purrr_bar(
        ae_per_visit, ls_study_ae_per_visit,
        .purrr = furrr::future_map2,
        .f = sim_heuristic_ur,
        .f_args = list(
          ur_rates = c(0, 0.1, 0.25, 0.5, 0.75, 1),
          .f = flag_heuristics_box
          ),
        .steps = nrow(.)
      )
    )
)

df_perf_heuristic_box <- df_perf_heuristic_box %>%
  select(sim) %>%
  unnest(sim) %>%
  group_by(ur_rate) %>%
  summarise(
    is_ur = sum(is_ur),
    n_sites = n(),
    .groups = "drop"
  ) %>%
  mutate(
    ratio = is_ur / n_sites,
    ratio_type = ifelse(ur_rate == 0, "fpr", "tpr"),
    ci95_low = map2_dbl(is_ur, n_sites, get_prop_test_ci95, ix = 1),
    ci95_high = map2_dbl(is_ur, n_sites, get_prop_test_ci95, ix = 2),
  )

readr::write_csv(df_perf_heuristic_box, file = "heuristic_box.csv")

df_perf_heuristic_box <- readr::read_csv(file = "heuristic_box.csv")

df_perf_heuristic_box %>%
  knitr::kable(digits = 3)

ur_rate	is_ur	n_sites	ratio	ratio_type	ci95_low	ci95_high
0.00	405	15674	0.026	fpr	0.023	0.028
0.10	599	15674	0.038	tpr	0.035	0.041
0.25	1612	15674	0.103	tpr	0.098	0.108
0.50	6619	15674	0.422	tpr	0.415	0.430
0.75	10754	15674	0.686	tpr	0.679	0.693
1.00	13408	15674	0.855	tpr	0.850	0.861

Plot Performance Metrics

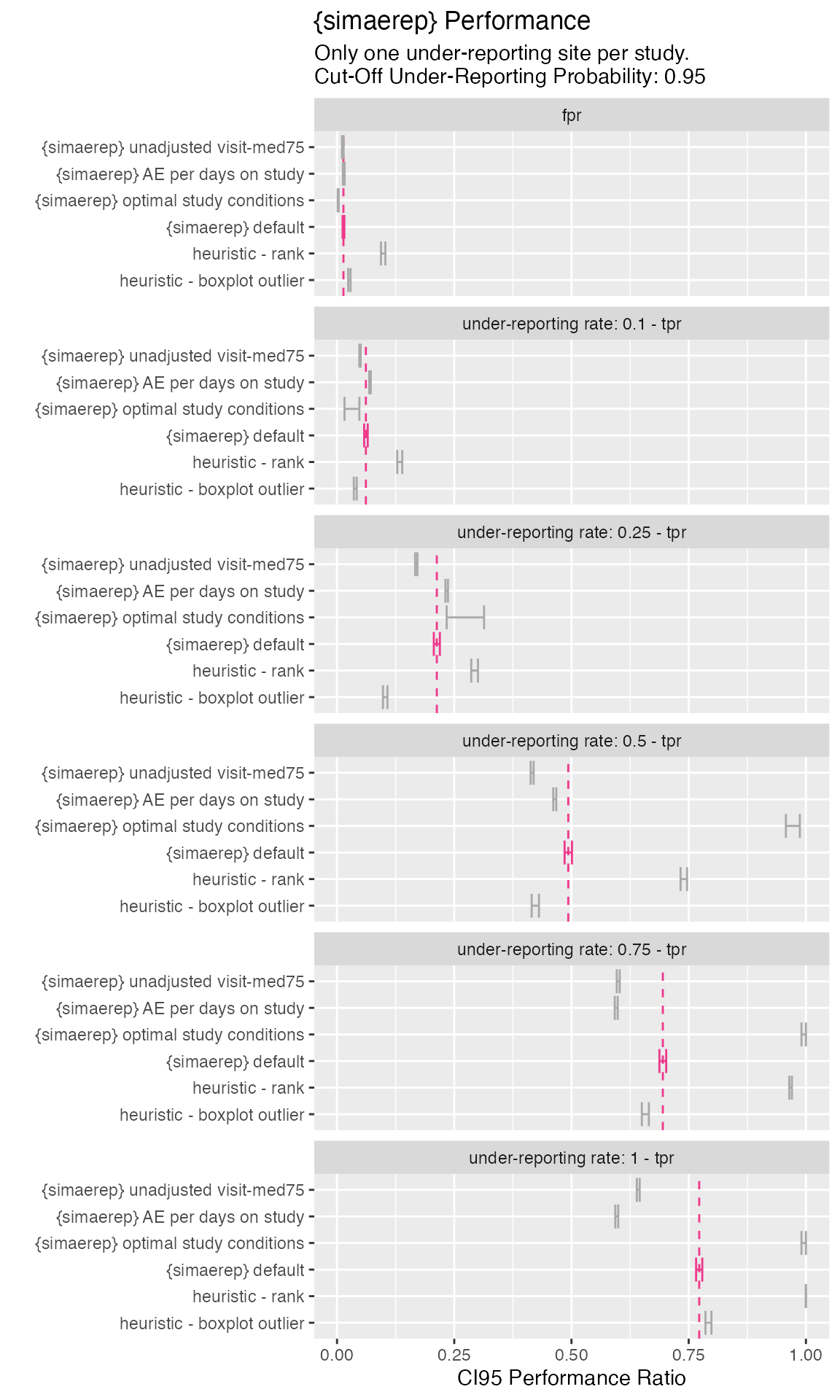
{simaerep} reduces the false positive rate compared to the heuristics.
Rank-based heuristics has higher true positive rates at the cost of higher false positive rates. Similar effects could be achieved by lowering the {simaerep} flagging threshold
Using AE per visits over AE per patient days has better performance.
Adjusting visit_med75 has also improved performance
{simaerep} results are closest to boxplot outlier heuristic but with better overall performance
under optimal conditions {simaerep} catches almost all under-reporting sites if under-reporting rate is greater 0.5

prep_for_plot <- function(df, type) {
  df %>%
    mutate(ur_rate = paste0("under-reporting rate: ",  ur_rate, " - ", ratio_type),
           ur_rate = ifelse(str_detect(ur_rate, "fpr"), "fpr", ur_rate)) %>%
    select(ur_rate, ratio_type, ratio, ci95_low, ci95_high) %>%
    mutate(type = type)
}

df_perf <- df_perf_st %>%
  filter(ur_rate == 0) %>%
  mutate(ratio_type = "fpr") %>%
  select(ur_rate, ratio_type, ratio = fpr, ci95_low = fpr_ci95_low, ci95_high = fpr_ci95_high) %>%
  bind_rows(
    df_perf_st %>%
      filter(ur_rate > 0) %>%
      mutate(ratio_type = "tpr") %>%
      select(ur_rate, ratio_type, ratio = tpr, ci95_low = tpr_ci95_low, ci95_high = tpr_ci95_high)
  ) %>%
  prep_for_plot(type = "{simaerep} optimal study conditions") %>%
  bind_rows(
    prep_for_plot(df_perf_portf, type = "{simaerep} default"),
    prep_for_plot(df_perf_portf_days, type = "{simaerep} AE per days on study"),
    prep_for_plot(df_perf_portf_old_visit_med75, type = "{simaerep} unadjusted visit-med75"),
    prep_for_plot(df_perf_heuristic_rnk, type = "heuristic - rank"),
    prep_for_plot(df_perf_heuristic_box, type = "heuristic - boxplot outlier"),
  ) %>%
  mutate(
    type = fct_relevel(type, c(
      "heuristic - boxplot outlier",
      "heuristic - rank",
      "{simaerep} default",
      "{simaerep} optimal study conditions"
      )
    )
  )


df_perf %>%
  mutate(color = ifelse(type == "{simaerep} default", "violetred2", "darkgrey"),
         ref = ifelse(type == "{simaerep} default", ratio, 0)) %>%
  group_by(ur_rate) %>%
  mutate(ref = max(ref)) %>%
  ggplot(aes(type, ratio)) +
    geom_hline(aes(yintercept = ref),
               linetype = 2,
               color = "violetred2") +
    geom_errorbar(aes(ymin = ci95_low, ymax = ci95_high, color = color)) +
    facet_wrap(~ ur_rate, ncol = 1) +
    scale_colour_identity() +
    coord_flip() +
    labs(
      x = "",
      y = "CI95 Performance Ratio", 
      title = "{simaerep} Performance",
      subtitle = "Only one under-reporting site per study.\nCut-Off Under-Reporting Probability: 0.95"
    )

df_perf %>%
  arrange(ur_rate, desc(type)) %>%
  select(ur_rate, type, ratio, ci95_low, ci95_high) %>%
  knitr::kable(digits = 3)

ur_rate	type	ratio	ci95_low	ci95_high
fpr	{simaerep} unadjusted visit-med75	0.001	0.000	0.001
fpr	{simaerep} AE per days on study	0.000	0.000	0.001
fpr	{simaerep} optimal study conditions	0.002	0.001	0.004
fpr	{simaerep} default	0.001	0.000	0.001
fpr	heuristic - rank	0.100	0.095	0.104
fpr	heuristic - boxplot outlier	0.026	0.023	0.028
under-reporting rate: 0.1 - tpr	{simaerep} unadjusted visit-med75	0.004	0.003	0.004
under-reporting rate: 0.1 - tpr	{simaerep} AE per days on study	0.006	0.006	0.007
under-reporting rate: 0.1 - tpr	{simaerep} optimal study conditions	0.028	0.016	0.048
under-reporting rate: 0.1 - tpr	{simaerep} default	0.005	0.004	0.006
under-reporting rate: 0.1 - tpr	heuristic - rank	0.136	0.131	0.142
under-reporting rate: 0.1 - tpr	heuristic - boxplot outlier	0.038	0.035	0.041
under-reporting rate: 0.25 - tpr	{simaerep} unadjusted visit-med75	0.038	0.037	0.040
under-reporting rate: 0.25 - tpr	{simaerep} AE per days on study	0.068	0.066	0.069
under-reporting rate: 0.25 - tpr	{simaerep} optimal study conditions	0.272	0.234	0.314
under-reporting rate: 0.25 - tpr	{simaerep} default	0.051	0.048	0.055
under-reporting rate: 0.25 - tpr	heuristic - rank	0.301	0.294	0.308
under-reporting rate: 0.25 - tpr	heuristic - boxplot outlier	0.103	0.098	0.108
under-reporting rate: 0.5 - tpr	{simaerep} unadjusted visit-med75	0.205	0.203	0.208
under-reporting rate: 0.5 - tpr	{simaerep} AE per days on study	0.238	0.235	0.241
under-reporting rate: 0.5 - tpr	{simaerep} optimal study conditions	0.976	0.957	0.987
under-reporting rate: 0.5 - tpr	{simaerep} default	0.267	0.260	0.274
under-reporting rate: 0.5 - tpr	heuristic - rank	0.750	0.743	0.757
under-reporting rate: 0.5 - tpr	heuristic - boxplot outlier	0.422	0.415	0.430
under-reporting rate: 0.75 - tpr	{simaerep} unadjusted visit-med75	0.390	0.387	0.393
under-reporting rate: 0.75 - tpr	{simaerep} AE per days on study	0.375	0.372	0.378
under-reporting rate: 0.75 - tpr	{simaerep} optimal study conditions	1.000	0.990	1.000
under-reporting rate: 0.75 - tpr	{simaerep} default	0.479	0.471	0.486
under-reporting rate: 0.75 - tpr	heuristic - rank	0.970	0.967	0.972
under-reporting rate: 0.75 - tpr	heuristic - boxplot outlier	0.686	0.679	0.693
under-reporting rate: 1 - tpr	{simaerep} unadjusted visit-med75	0.478	0.475	0.482
under-reporting rate: 1 - tpr	{simaerep} AE per days on study	0.406	0.402	0.409
under-reporting rate: 1 - tpr	{simaerep} optimal study conditions	1.000	0.990	1.000
under-reporting rate: 1 - tpr	{simaerep} default	0.587	0.580	0.595
under-reporting rate: 1 - tpr	heuristic - rank	1.000	1.000	1.000
under-reporting rate: 1 - tpr	heuristic - boxplot outlier	0.855	0.850	0.861

plan(sequential)